Wie löse ich aufgabe 3 😭😭?

3 Antworten
Lesen sollte schon reichen, da musst Du nicht mal wirklich rechnen.
Auf der Dose steht, für wie viele qm sie reicht: 7
Wie viele qm (in etwa) fallen bei dem Tisch an?
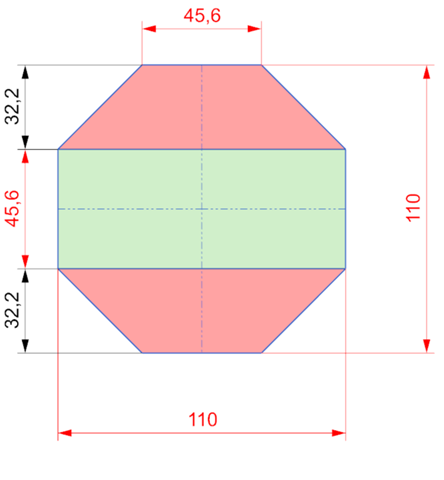
Aufgabe 3
4 Rechtecke (grün)
A1 = 110 * 45,6 * 4
A1 = 20064 cm²
---
8 Trapeze ( rot)
A2 = (((110 - 45,6) / 2) + 45,6) * 32,2 * 8
A2 = 20041,28 cm²
---
Gesamtflächen A
A = A1 + A2
A = 20064 + 20041,28
A = 40105,28 cm²
A = 4,011 m²
Ein Dose reicht.

Super.
Ich bin da pragmatischer unterwegs. 110x110 = etwas mehr als 2, aber deutlich weniger als 3 qm. Zwei Seiten - höchstens 6 qm. Die Dose gibt 7 qm her. Die Frage ist somit schon beantwortet.
Wie viel Rest bleibt, ist nicht gefragt und ohnehin sinnfrei, weil der Azubi, der das Teil streichen soll, sich nach 14 Minuten den Daumen verstaucht und sieben Wochen ausfällt.
Der Kunde zieht den Auftrag zurück. Bilanz: Eine angebrochene Dose Farbe, die niemand mehr nutzt = Sondermüll.
Die eine Seite des Achtecks ist 45,6 cm lang, nicht 15,6 cm.
Aber am Ergebnis ändert sich nichts.
Wäre der Tisch einfach nur ein Quadrat mit Seitenlänge 1,1 m, wäre ein beidseitiger, doppelter Anstrich mit einer Dose für 7 m² locker drin, weil die gesamt anzupinselnde Fläche weniger als 5 m² betragen würde.
Fehlen dann an den Ecken noch Dreieck, sodass ein Achteck entsteht, reicht es natürlich allemal.
Ich vermute, dass gfntom Recht hat und auf dem Bild neben der Dose, die wir sehen, noch eine kleinere Dose steht.
Ich sag mal so, wenn der FS zu doof ist, die Angabe komplett zu zeigen, wundert es mich nicht, dass es mit der Rechnung hapert...
Du machst auch eine Annahme, die zwar in der Praxis vernünftig ist, aber die man eigentlich nicht als gegeben nehmen darf, nämlich, dass die 15,6 cm (eigentlich 45,6 cm) mittig liegen.
Letztenendes ist das aber egal, weil sich die Fläche nicht ändert, wenn die Position anders ist.
Das viel größere Problem ist, dass aus dem Bild genaugenommen nicht hervorgeht, dass die anderen Seiten auch alle 15,6 cm (eigentlich 45,6 cm) lang sind.
Bei echten Tischen würde man das wohl so machen, aber "wird wohl schon so sein", ist eigentlich nicht die übliche Herangehensweise in der Mathematik.
Hier hätte aus der Angabe hervorgehen sollen, dass dem so ist (z.B. direkt oder mit dem Hinweis auf zwei Symmetrieachsen o.ä.).
Fazit: Die Aufgabenstellung ist schlampig, daher darf man wohl die erwähnten Annahmen machen, weil die Aufgabe sonst unlösbar wäre.
Die Aufgabe ist schlampig gestellt (s. mein Kommentar bei merkurus).
Ich würde sie wiefolgt lösen (mit der Annahme, dass die vier Seiten, die in der Abbildung waagrecht bzw. senkrecht sind, alle gleich lang sind, d.h. 45,6 cm).
Da sich die Fläche eines Trapzes nicht ändert, wenn man die parallelen Seiten verschiebt (solange sich der Abstand nicht ändert), kann man gedanklich die Tischkante links und rechts z.B. so nach unten "ziehen", dass die beiden Dreiecke unten verschwinden, dafür die beiden oberen Dreiecke größer werden.
Man hat dann ein Quadrat mit der Fläche (1,1 m)², in dem zwei Dreiecke mit derselben Fläche fehlen.
Diese Fläche berechnet sich aus:
Das ergibt eine Tischoberfläche von 10.026,32 cm², also ganz knapp über 1 m².
Für einen doppelten, beidseitigen Anstrich benötigt man Farbe für die vierfache Fläche.
sieht für mich so aus, als ob die Dose für 7 m² die "große" Dose wäre.
Daneben steht (am Bild abgeschnitten) wohl die kleinere.