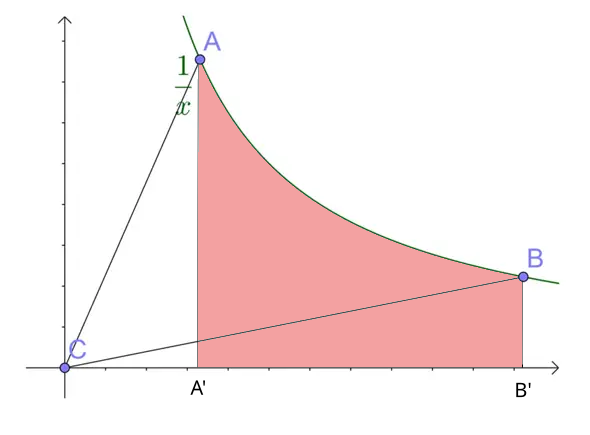
Wie berechnet man diese Fläche?

Ich sehe einfach den Wald vor lauter Bäumen nicht. Ist die krummlinig begrenzte Fläche mit den Eckpunkten A (a, 1/a) B (b, 1/b) und C(0,0) einfach ein wahnsinnig hässlicher Ausdruck, oder geht das irgendwie ganz einfach? Ideen habe ich schon zur Berechnung, aber das führt mich immer auf riesige Terme…

Answer 1

[mihisu]

Die Ursprungsgerade CA lässt sich duch...

$y=\frac{y_A}{x_A}\cdot x=\frac{\ \frac{1}{a}\ }{a}\cdot x=\frac{1}{a^2}\cdot x$

... und die Ursprungsgerade CB lässt sich durch...

$y=\frac{y_B}{x_B}\cdot x=\frac{\ \frac{1}{b}\ }{b}\cdot x=\frac{1}{b^2}\cdot x$

... beschreiben.

Ich würde nun die gesuchte Fläche in zwei Teilflächen unterteilen...

... und diese dann mit Hilfe von Integralrechnung berechnen, indem die Differenz (oberer Funktionswert - unterer Funktionswert) im entsprechenden Intervall integriert wird.

$F_1=\int\limits_{0}^{a} \left(\frac{1}{a^2}\cdot x-\frac{1}{b^2}\cdot x\right)\,\text{d}x$

$F_1=\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\cdot \int\limits_{0}^{a} x\,\text{d}x$

$F_1=\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\cdot \left[\frac{x^2}{2}\right]_0^a$

$F_1=\left(\frac{1}{a^2}-\frac{1}{b^2}\right)\cdot \frac{a^2}{2}$

$F_1=\frac{1}{2}-\frac{1}{2}\cdot \frac{a^{2}}{b^2}$

$F_2=\int\limits_{a}^{b} \left(\frac{1}{x}-\frac{1}{b^2}\cdot x\right)\,\text{d}x$

$F_2=\left[\ln(x)-\frac{1}{b^2}\cdot \frac{x^2}{2}\right]_{a}^{b}$

$F_2=\ln(b)-\frac{1}{b^2}\cdot \frac{b^2}{2}-\left(\ln(a)-\frac{1}{b^2}\cdot \frac{a^2}{2}\right)$

$F_2=\ln(b)-\frac{1}{2}-\ln(a)+\frac{1}{2}\cdot \frac{a^2}{b^2}$

$F_\text{ges}=F_1+F_2$

$F_\text{ges}=\frac{1}{2}-\frac{1}{2}\cdot \frac{a^2}{b^2}+\ln(b)-\frac{1}{2}-\ln(a)+\frac{1}{2}\cdot \frac{a^2}{b^2}$

$F_\text{ges}=\ln(b)-\ln(a)$

Ergebnis: Der gesuchte Flächeninhalt ist ln(b) - ln(a).

Comments

[eterneladam]

... und damit verblüffenderweise gleich dem Integral über 1/x in diesen Grenzen.

Die Dreiecke (0,0) - (a,0) - (a,1/a) bzw. (0,0) - (b,0) - (b,1/b) haben jeweils Fläche gleich 1/2, den Flächenanteil im kleinen Dreieck links unten haben sie gemeinsam, deshalb ist F1 gleich der Fläche unter CB in den Integrationsgrenzen, deshalb das Ergebnis.

[hannes45451]

Herzlichen Dank für die ausführliche und sehr gut verständliche Antwort!

Answer 2

[VeryBestAnswers]

Hier gibt es eine sehr elegante Lösung! Wir beginnen damit, diese Fläche mit dem Integral der Funktion zu berechnen:

Dazu brauchen wir die Formel:

$f\left(x\right)=\frac{1}{x}$ $F\left(x\right)=\ln\left(x\right)$

Das heißt, die Fläche ist

$\ln\left(b\right)-\ln\left(a\right)$

Dazu müssen wir jetzt die Fläche des rechtwinkligen Dreiecks daneben addieren, und das Dreieck darunter abziehen. Die Fläche eines rechtwinkligen Dreiecks ist die Hälfte von der Grundfläche mal Höhe:

$\Delta CA'A\ =\ \frac{1}{2}\cdot a\cdot f\left(a\right)=\frac{1}{2}\cdot a\cdot\frac{1}{a}=\frac{1}{2}$ $\Delta CB'B\ =\ \frac{1}{2}\cdot b\cdot f\left(b\right)=\frac{1}{2}\cdot b\cdot\frac{1}{b}=\frac{1}{2}$

Das heißt, die gesuchte Fläche ist

$\ln\left(b\right)-\ln\left(a\right)+\frac{1}{2}-\frac{1}{2}\ =\ \ln\left(b\right)-\ln\left(a\right)$