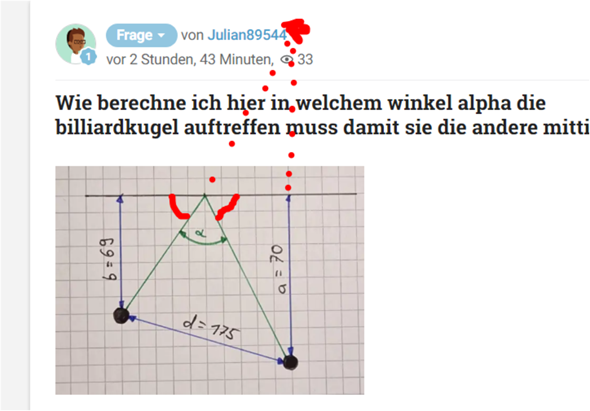
Wie berechne ich hier in welchem winkel alpha die billiardkugel auftreffen muss damit sie die andere mittig trifft?

Links soll es nicht etwa 49 heißen?
Nein die zahlen stimmen so
2 Antworten
Spiegle die zweite Kugel an der Bande und verbinde dann die erste Kugel mit dem Spiegelbild.
Die grüne Bahn verläuft wie ein Lichtstrahl im Spiegel (=Bande): Einfallswinkel=Ausfallswinkel.
Verlängere also die blaue Strecke rechts (a=70) nach oben um die gleiche Distanz. Dort liegt das Spiegelbild der rechten Kugel, und von der linken Kugel aus hast Du einen geraden Blick darauf. Der scheinbare Blick startet wie die grüne Linie, geht aber durch die Bande weiter zum Spiegelbild.
In der Realität wird diese Gerade natürlich – wie eingezeichnet – an der Bande reflektiert. Die Winkel rechts und links von 𝛼 sind dann gleich groß. Das passt in Deiner Skizze nicht so ganz.
ich habe in meiner Antwort deine Worte in eine Skizze umgesetzt. Schau bitte mal nach
Und wie kommt man nun rechnerisch ab Alpha ?
Ups, ich sehe gerade, dass das Spiegeln nur gut ist, um die Bahn zu konstruieren. Zum Berechnen braucht man nur „Einfallswinkel=Ausfallswinkel“. Der sei 𝛾 (in Deiner Skizze rot).
Es gibt zwei ähnliche rechtwinklige Dreiecke mit je einer Kugel als Ecke und der Bande als Kathete. Die Länge der beiden Katheten zusammen verrät uns Pythagoras: √(175²−1²). Die verteilt sich 69:70 auf die beiden Dreiecke. Also:
tan 𝛾 = 70 / [ √(175²−1²)·70/139 ] = 139/√(175²−1²)
Und zum Schluss 𝛼 = 180° − 2𝛾.
[Ich komme da auf 𝛼≈103°]
das mit dem Konstruieren habe ich auch so gesehen . Da freut man sich doch , wenns bestätigt wird.
ich habe mal die Worte von ralphdieter versucht in eine Skizze umzusetzen

die beiden Winkel sollten gleich groß sein.
aber ich habe keine Idee ,wie man nun rechnerisch an alpha kommen kann.
Ich begreiffe es leider nicht. Kannst du mir das genauer erklären?