Welche Funktion ist invertierbar?
Lerne gerade für meine Mathe Prüfung. Die Frage ist welche Funktion invertierbar ist.
Die richtige Antwort ist anscheinend die 2. Möglichkeit, jedoch verstehe ich nicht wie.
Wenn die Funktion nur die natürlichen Zahlen und die 0 umfasst, wie kann diese dann invertierbar sein. Negative Zahlen sollte man doch nicht einsetzen können oder liege ich falsch. Was ist dann das neutrale Element?
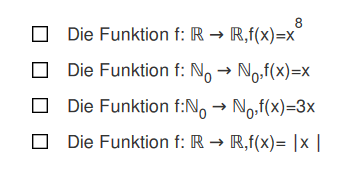
3 Antworten
Eine Funktion muss jedem Argument x eindeutig einen Funktionswert zuordnen. Das machen die vier hier genannten Funktionen.
Wenn sie invertierbar ist, dann muss sich aus dem Funktionswert auch eindeutig ein Argument zuordnen lassen.
f(x) = x^8 liefert für x = 2 und für x = -2 eindeutig f(x) = 256. Aber aus f(x) = 256 kann man nicht eindeutig das x rekonstruieren.
(f(x) = x^7 ist z.B. invertierbar.)
Die Betragsfunktion hat das gleiche Problem.
f(x) = 3x ist zwar eine Funktion, die im Bereich der reellen Zahlen invertierbar ist. Im Bereich der natürlichen Zahlen gibt es aber das Problem, dass man z.B. für f(x) = 4 kein passendes x findet.
f(x) = x ist garantiert invertierbar. Sie ist sogar mit ihrer Umkehrfunktion identisch.
Da hast Du natürlich Recht. An solche Spitzfindigkeiten hatte ich jetzt nicht gedacht 😉
Spizfindig ist sicher übertrieben ausgedrückt, aber Mathematik ist eben knallhart.
Wenn die Funktion nur die natürlichen Zahlen und die 0 umfasst, wie kann diese dann invertierbar sein. Negative Zahlen sollte man doch nicht einsetzen können oder liege ich falsch. Was ist dann das neutrale Element?
Ich glaube du hast nicht verstanden, was invertierbar bedeutet. Hier geht es nicht darum, dass ob der Definitionsbereich eine Gruppe ist, sondern ob die Funktion bijektiv ist.
Eine Funktion bist bijektiv, wenn sie injektiv und surjektiv ist.
Eine Funktion ist injektiv, wenn aus f(x)=f(y) folgt, dass x=y gilt. (Oder dass jedes Element des Zielbereiches höchstens ein Urbild hat)
Eine Funktion ist surjektiv, wenn es für jedes y aus dem Zielbereich ein x aus dem Definitionsbereich gibt, sodass f(x)=y gilt (also dass jedes Element aus dem Zielbereich mindestens ein Urbild hat)
Das ist bei der 2. Funktion der Fall.
Die erste Funktion bist zum Beispiel nicht invertierbar, da sie nicht bijektiv ist. Es gilt zum Beispiel f(1) = f(-1)
Nur die zweite Funktion ist invertierbar.
Eine Besonderheit der zweiten Funktion ist, dass sie zu sich selbst invers ist - das hat man nicht oft.
Die dritte Funktion wäre als Abbildung von Q nach Q und auch als Abbildung von R nach R invertierbar. Du hast richtig erkannt, dass hier die Beschränktung auf N0 die Invertierbarkeit verhindert.
Die zweite Funktion ist invertierbar, weil sie jedes Element aus der Definitionsmenge auf sich selbst abbildet und Definitions- und Wertemenge gleich sind. Da ist der "Rückweg" vom Funktionswert zum Funktionsargument dann einfach und vor allem auch immer möglich.
Beachte bitte, dass Invertierbarkeit nichts mit Steigkeit zu tun hat und auch nichts damit, ob du eine "einfache Funktionskurve" hast. "Einfache Funktionskurve" ist sowieso kein mathematischer Begriff, sondern ein Ausdruck, der nur dann vorkommen kann, wenn die Begriffe fehlen.
Der Begriff "neutrales Element" hat mit Invertierbarkeit nichts zu tun - er beschreibt eine Eigenschaft bei gewissen Rechenoperationen.
Auf Schulniveau wird über Invertierbarkeit in der Regel oft so entschieden, dass man prüft, ob man eine Funktionsdefinition erhält, wenn man die Funktion y=f(x) nach x auflöst und Definitions- und Wertebereich vertauscht.
Ein anderes schulübliches Kriterium ist, sich zu überlegen, ob man den Funktiongraph an der der 45°-Geraden (also der Geraden durch den ersten und den dritten Quadranten des Koordinatensystems; Geradengleichung: y = x) spiegeln kann und dabei wieder ein Funktionsgraph entsteht, für den überdies gilt, dass alle Funktionswerte im Definitionsbereich der nicht invertierten Funktion liegen.
Das stimmt aber nur wenn der Wertebereich und der Zielbereich identisch sind. Wäre es zum Beispiel eine Funktion von N nach Z wäre die Funktion nicht invertierbar.