warum ist 𝑔(𝑥)= -3/x punktsymmetrisch zum Ursprung?

Man rechnet ja mit dem Ansatz g(-x).

Also: g(-x)= -3/-x= 3/x. Aber da kommt doch nicht -g(x) raus, sondern g(x)

Answer 1

[ghul666]

Punktsymmetrie heißt hier

$f\left(-x\right)=-f\left(x\right)$

Und das kommt ja hin.

Comments

[ZeroTwo432]

ahh also müsste man theoretisch nichts rechnen, weil schon die Funktion verratet, welche Symmetrie sie hat?

[ghul666]

@ZeroTwo432

Diese Funktion ist ja sehr simpel aufgebaut.

Hier kann man sofort erkennen, dass sie das Vorzeichen ändert, wenn man -x einsetzt.

[Halbrecht]

@ZeroTwo432

wenn man weiß , dass es so ist , hilft das , die eigene Lösung zu kontrollieren

in der Arbeit reicht es aber nicht

Answer 2

[DerRoll]

Beachte die Bruchrechenregeln und die Regeln für das Rechnen mit negativem Vorzeichen:

3/x = -(-3/x), also g(-x) = -g(x).

Answer 3

[Halbrecht]

Man rechnet ja mit dem Ansatz g(-x)

richtig
Das wäre hier -3/-x = 3/x

aber geprüft wird das mit - ( f(x) ) und das wäre - ( -3/x ) , was aber 3/x ist

Answer 4

[verreisterNutzer]

Musst Du nur prüfen, ob g(x) = - g(x) ist (und das ist der Fall)

$g\left(-x\right)=-\frac{3}{\left(-x\right)}=\frac{3}{x}=-\ g\left(x\right)\ \ \left(-\left(-\frac{3}{x}\right)\right)$

Skizze:

Answer 5

[Alex7264]

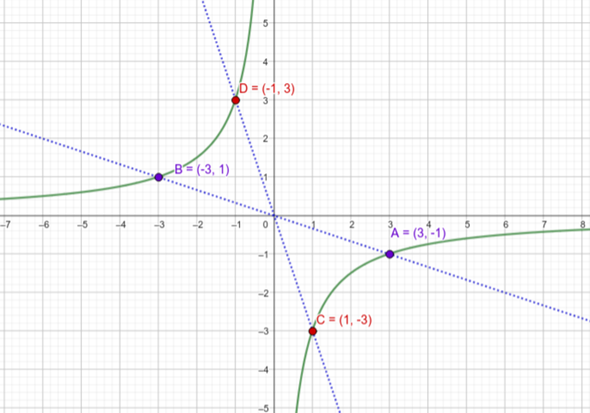
Du hast es richtig vorgerechnet: g(-x) = -3/-x = 3/x

Deine Funktion g(x) lautet: g(x) = -3/x

-g(x) wäre dann: -g(x) = - (- 3/x) = 3/x

(zweimal Minus hebt sich auf und du bekommst bei -g(x) genau das, was du oben ausgerechnet hast, nämlich 3/x)