Wann kann man endlich mit einem Flugzeug Lichtjahre weit reisen?
Ja, Lichtjahre ist viel, aber irgendwann kann man doch bestimmt 1 Lichtjahr weit reisen, oder?
23 Antworten
Bis auf weiteres nicht, in den nächsten Jahrhunderten.
Dem Grunde nach fehlt die Energie um etwa ein Raumschiff mit Lichtgeschwindigkeit anzutreiben.
Zudem fehlte es an einem Ziel.
In Reichweite eines Lichtjahres ist nichts, in der Art eines erdähnlichen Planeten.
Am nächsten dran wäre eventuell Proxima Centaueri b, schlappe 4,5 Lichtjahre entfernt,nur für den Hinweg.
Falls man zuückkehren wollte, wäre der Energiebedarf entsprechend größer.
Zudem das Problem mit der Nutzlast.
Je mehr transportiert werden müsste, je größer der Energiebedarf.
In der Sci Fi ist das möglich, in der geltenden Physik nicht.
- a) die Nutzlast
willst Du nur 10 Menschen transsportieren ist das eine Melodie,
entsprechend eine andere bei 100, 1000 oder gar mehr
- b) keine Reise ohne Ziel, gell
auf 1 Lichtjahr Entfernung befindet sich gar nichts
erfähnliches, frühester Halt Proxima Centauri b, schlappe 4,5
Lichtjahre
Willst dort zu Lebzeiten ankommen, mit Unterlichtgechwindkeit, wird es schon eng und zudem ein Never Comback Flug.
Du solltest nicht komplett unterschiedliche Themen vermischen!
Beim Nutzlast-Problem geht es um die Schwierigkeit, eine bestimmte (Unterlicht)geschwindigkeit relativ zum Ausgangsort überhaupt zu erreichen, z.B. 0,1c, 0,6c oder gar 0,8c.
Deine eigentliche Behauptung ist aber, mit Unterlichtgeschwindigkeit (und selbst 0,8c ist Unterlichtgeschwindigkeit) würde man z.B. α Centauri nie erreichen können, und das ist falsch.
Nur wenn man zu langsam ist, um das Sonnensystem zu verlassen, kann man das nicht.
Wieder eine andere Frage ist, welche Geschwindigkeit man bräuchte, um z.B. α Centauri zu eigenen Lebzeiten zu erreichen - immer gesetzt den Fall, dass man sie erreichen kann, wie auch immer.
Und selbstverständlich muss das nicht Lichtgeschwindigkeit sein. Schon mit 0,2c könnte man in 22½ Jahren (Δt, also Erdzeit!) zu α Centauri, mit 0,6c in Δt=8½ Jahren, es wären Δτ=6 Jahre.
Mit 0,8c würde man Δt=5⅝ Jahre brauchen und Δτ=3⅜ Jahre - weniger als Δs/c!
Ein Lichtjahr sagt ja bereits, dass das Licht selbst ein Jahr benötigt.
Selbst wenn das "Flugzeug" Lichtgeschwindigkeit hat braucht es 1 Jahr.
Darum wäre der "heilige Grahl" in dem Gebiet ja die Entdeckung des Warp antriebs.
Selbst wenn das "Flugzeug" Lichtgeschwindigkeit hat…
Das ist nicht möglich, weil es dann sogar relativ zu sich selbst mit Lichtgeschwindigkeit fliegen müsste.
…braucht es 1 Jahr.
Erdzeit respektive Koordinatenzeit irgendeines Objekts, das man als halbwegs stationär betrachten kann.
Bordzeit würde es mit (fast) genau c (fast) gar keine brauchen.
Das ist nicht möglich, weil es dann sogar relativ zu sich selbst mit Lichtgeschwindigkeit fliegen müsste.
Das es möglich ist habe ich nicht gesagt. Die gewählte Ausdrucksweise mit "Selbst wenn" war schon so gewählt, dass damit implizit angedeutet werden sollte, dass das nicht möglich ist.
Erdzeit respektive Koordinatenzeit irgendeines Objekts, das man als halbwegs stationär betrachten kann.
Das ist eine Vorraussetzung für die Angabe ja.
Bordzeit würde es mit (fast) genau c (fast) gar keine brauchen.
Richtig, Erdzeit allerdings schon.
Lichtjahre ist eine Entfernung, sie entspricht der Entfernung die das Licht in einen Jahr zurück legt.(
9,46 Billionen Kilometer)
Ich vermute mal du meinst Lichtgeschwindigkeit.
Zum aktuellen Zeitpunkt ist es nicht mal ansatzweise möglich so schnell wie das Licht zu fliegen.
E = m x c^2
Die Formel von Einstein. Aus dieser kann man die Energie berechnen die du brauchst um etwas auf Lichtgeschwindigkeit zu beschleunigen.
Selbst wenn es möglich wäre, würde kein Mensch diese Beschleunigung überleben.
Natürlich geht auch eine langsamere Beschleunigung, aber das würde wieder zu lange dauern.
Eine Möglichkeit die realistisch ist, wär aus der Serie Star Trek der Warp Antrieb. Damit wäre es möglich sogar schneller als das Licht zu fliegen, aber dafür wär sehr viel mehr Anti-Materie nötig als das was bisher je auf der Erde durch Teilchenbeschleuniger hergestellt wurden.
"würde kein Mensch diese Beschleunigung überleben"
Das stimmt so nicht unbedingt. Ich muss ja nicht wie in einer Kanone a la Jules Verne beschleunigen. Theoretisch könnte die Beschleunigungsstrecke ja auch unendlich lang sein.
Deshalb kann ich ein Raumschiff durchaus auch mit nur 1g beschleunigen. Je geringer die Beschleunigung, desto länger dauert es natürlich bis ich auf einen vernünftige Geschwindigkeit komme.
Dazu gibt es ja in der Literatur Berechnungen.
Die Zunahme der relativistischen Masse mit dem gegen Unendlich gehenden Energiebedarf lassen wir dabei noch unberücksichtigt.
Doch, nämlich indirekt durch die Energie, die zur relativistischen Massenzunahme führt.
Aber genau so hat es der Ratgeber ja schon beschrieben.
Hallo Toukina,
wenn ein Flugzeug etwa siebeneinhalb mal um die Erde fliegt, hat es eine Lichtsekunde zurückgelegt - relativ zur Erde und vorwiegend im Kreis, wodurch es sich - in Bezug auf die Erde - vom Ausgangsort nicht besonders entfernt. Das würde es auch nicht, wenn es rund 220 Millionen mal um die Erde fliegen würde (lange vorher würde es wohl auseinanderfallen), was rechnerisch etwa einem Lichtjahr entspräche.
Man kann im Prinzip auch ein Flugzeug in den Weltraum schießen wie die Firma Tesla einen ihrer Roadster, was aber ungleich teurer und aufwändiger wäre. Vor allem müsste man (vorzugsweise mit Hilfe von Swing-by-Manövern) genug kinetische Energie aufnehmen, um das Sonnensystem verlassen zu können, und dann wäre es nur mehr eine Frage der Zeit, sich um ein Lichtjahr oder mehr von der Erde zu entfernen. Einer sehr langen Zeit, im Zweifelsfall, und eventuelle Menschen an Bord würden nicht einmal den Anfang der Reise überleben, zumal ein Flugzeug für eine Weltraumreise ungeeignet ist.
Für einen Flug über Lichtjahre bräuchte man ein Raumschiff, das groß genug ist, ein ganzes Ökosystem zu fassen, mit einer Energiequelle, die zuverlässig funktioniert, denn die Reisenden müssen sich selbst versorgen können.
Im Prinzip ist so ein Raumschiff die Erde selbst, mit der Sonne als der zuverlässigen Energiequelle. Das gesamte Sonnenystem fliegt mit etwa 250km/s≈8,33×10⁻⁴c um das Zentrum der Milchstraße herum und legt ein Lichtjahr in etwa 1200 Jahren zurück - relativ zur Milchstraße.
Relativ zum Kosmischen Hintergrund (cosmic microwave background, CMB) ist die Geschwindigkeit noch größer, knapp 370km/s≈1,2×10⁻³c, wodurch das Sonnensystem, falls es diese Geschwindigkeit beibehält, nur etwa 830 Jahre braucht, um relativ zum CMB ein Lichtjahr zurückzulegen. Das gilt natürlich auch für ein foiegendes, aber ebenso für ein im Hangar oder Museum stehendes Flugzeug.
Das ist dann natürlich kein interstellarer Flug oder Ähnliches, denn die „benachbarten“ Sternsysteme machen diese Bewegung mit.
Um so etwas zu bewerkstelligen, muss man tatsächlich ein Raumschiff bauen, das sowohl groß genug als auch antriebsstark genug ist, um die nötige Energie zu gewinnen und schnell genug zu sein. Um - relativ zur Erde - beispielsweise 0,6c zu erreichen, muss das Schiff 25% seiner Ruheenergie mc² (m Masse des gesamten Schiffs) zusätzlich als kinetische Energie aufnehmen, da das Verhältnis von Gesamtenergie durch Ruheenergie, der LORENTZ-Faktor
(1.1) γ := 1/√{1 – (v/c)²} = 1/√{1 – 0,36} = 1/√{0,64} = 1/0,8 = 1,25
ist, wobei c die Lichtgeschwindigkeit ist. Das ist eine ganze Menge, aber es ist nicht grundsätzlich unmöglich, dass man dieses Problem in den Griff bekommt. Swing-by-Manöver werden allerdings nicht reichen. Bei einem derartigen Tempo ist auch das Verhältnis zwischen Koordinatenzeit Δt und Eigenzeit Δτ wesentlich von 1 verschieden, nämlich
(1.2) Δt/Δτ = γ = 1,25 bzw. Δτ = 0,8·Δt
Dadurch erlebt jemand, der mit dem Raumschiff unterwegs ist, weniger Zeit, oder, wie man auch sagen kann, er legt die entsprechende Strecke in kürzerer Eigenzeit zurück. Wegen dieses oft irreführenderweise „Zeitdilatation“ genannten Phänomens könnte man mit genügend kinetischer Energie eine beliebige Strecke Δs in beliebig kurzer Eigenzeit zurücklegen - und gleichzeitig so schnell in die Zukunft katapultiert, dass der Quotient
(2) (Δs/Δτ)/(Δt/Δτ) = Δs/Δt
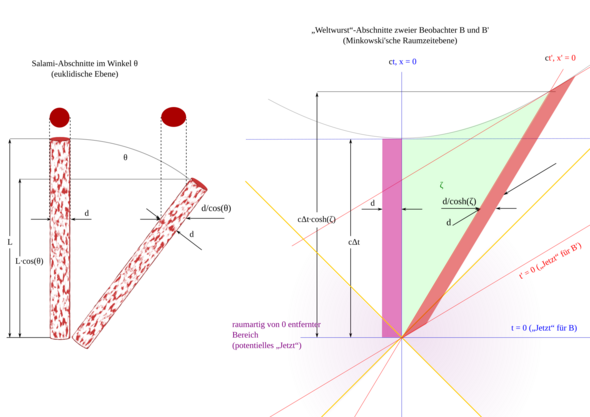
immer unter c bleibt. Die Eigenzeit selbst ist eine (absolute) Entfernung in der Raumzeit, gegeben durch die MINKOWSKI-Formel
(3) Δτ = √{Δt² – Δs²/c²},
die an den Satz des PYTHAGORAS erinnert.



OMG so viel! Kannst du meine frage beantworten? Wie viel kilometer sind ein Lichtjahr? Ein flugzeug fliegt ungefähr 800 kmh schnell. Es muss auch landen zum tanken. Also wenn man ständig fliegen würde, so wie Piloten es tum kommt man vielleicht auf eine Durschnittsgeschwindigkeit von 500 kmh über das jahr verteilt. Also wenn man immer nur fliegt, von flugzeug zu flugzeug umsteigt und quasi am flughafen lebt. Wie lange würde man für ein Lichtjahr brauchen bei einer Durchschnittsgeschwindigkeit von 500 kmh?
Man kann immer Lichtjahre weit reisen: mit einer Rakete, einem Flugzeug, mit dem Fahrrad, zu Fuß.
Es sollte mittlerweile zum Grundlagenwissen gehören, dass "Lichtjahr" eine Entfernung ist, und jede Entfernung kann ich mit jedem beliebigen Fortbewegungsmittel zurücklegen. Die Frage ist nur, wie lange es jeweils dauert.
OK, durchs Vakuum wird es - außer mit einer Rakete - etwas schwierig, aber das ändert nichts am Prinzip. Ich kann auch mein Fahrrad auf eine Geschwindigkeit beschleunigen, mit der es das Sonnensystem verlassen und z. B. zur Oort'schen Wolke (ca. 1 LJ (0,5 bis 1,5 LJ) entfernt) fliegen kann.
Nehmen wir die Wolke als Ziel und ein (unbemanntes) Raumschiff, dass etwa 10 bis 12 Prozent der Lichtgeschwindigkeit erreicht (wie z. B. das Projekt DAEDALUS der British Interplanetary Society, die ingenieurmäßig bisher immer noch beste Studie), würde es immer noch zwischen acht und zwölf Jahre dauern. Und dann?
Mit vier Beschleunigungsphasen (je 2x Gas geben und abbremsen) für Hin- und Rückflug plus Forschung wären Astronauten in einem vergleichbaren Raumschiff vielleicht 30 Jahre unterwegs. Wen würden hier auf der Erde die persönlichen Eindrücke noch interessieren?
Das können nach dem heutigen Stand der Technik, der Raumfahrtmedizin, der Psychologie automatische Sonden (die von DAEDALUS transportiert würden), viel besser. Sie hätten nach 12 Jahren ihr Ziel erreicht und würden (auch während der ereignislosen Reise) kontinuierlich Daten senden. Und wenn sie verloren gehen würden, was soll's?
Daran fehlt es immer, denn um c zu erreichen, wäre ∞ viel Energie nötig.
Aber wer sagt denn, das Raumschiff solle Lichtgeschwindigkeit haben? Der FS jedenfalls nicht.