Wie berechnet man Volumen und Oberfläche eines Kristalls?
Hey!
Ich benötige dringend Hilfe bei dieser Aufgabe. Verstehe nicht genau wie ich vorgehen soll.
Die Aufgabe lautet:
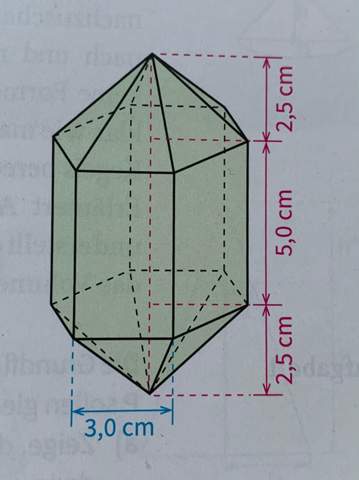
Einige Kristalle haben die Form eines regelmäßigen sechsseitigen Prismas mit aufgesetzten Pyramiden. Berechne Volumen und Oberflächeninhalt des Kristalls.
Habt ihr Ideen oder einen Ansatz?
Danke schonmal im Voraus!
:)
6 Antworten
Das Volumen des Prismas ist gleich Grundseite mal Höhe.
Du musst also zuerst den Flächeninhalt der Vielecke ausrechnen, die die Querschnitte des Prismas bilden.
A_Vieleck = n * a² / (4 * tan(180° / n))
Also gilt für das Volumen des Prismas :
V_Prisma(Vieleck) = n * a² / (4 * tan(180° / n)) * h_Prisma
Für das Volumen der gleichseitigen, regelmäßigen, regulären n-seitige Pyramiden gilt :
V_Pyramide = (1 / 3) * (n / 4) * a² / tan(180° / n) * h_Pyramide
Nun zur konkreten Rechnung :
n = 6
h_Prisma = 5 cm
a = 3 cm
h_Pyramide = 2,5 cm
A_Vieleck = 6 * 3² / (4 * tan(180° / 6)) = 23,383 cm²
V_Prisma(Vieleck) = 6 * 3² / (4 * tan(180° / 6)) * 5 = 116,913 cm³
V_Pyramide = (1 / 3) * (6 / 4) * 3² / tan(180° / 6) * 2.5 = 19,486 cm³
Man hat 1 Prima und 2 Pyramiden, also :
116,913 cm³ + 2 * 19,486 cm³ = 155,885 cm³
Mit Hilfe der folgenden Rechner kannst du das Ergebnis auch nachprüfen :
https://rechneronline.de/pi/sechseck.php
https://rechneronline.de/pi/regelmaessige-pyramide.php
Mantelfläche des vieleckigen Prismas :
M_Prisma(Vieleck) = n * a * h_Prisma
Mantelfläche der Pyramide :
G = (n / 4) * a² / tan(180° / n)
M_Pyramide = √(n * tan(180° / n) * G * h² + G²)
Konkrete Rechnung :
M_Prisma(Vieleck) = 6 * 3 * 5 = 90 cm²
G = (6 / 4) * 3² / tan(180° / 6) = 23,383 cm²
M = √(6 * tan(180° / 6) * 23.383 * 2.5² + 23.383²) = 32,450 cm²
O_Gesamt = 90 cm² + 2 * 32,450 cm² = 154,9 cm²
vielleicht hilf die Formel hier Regelmäßiges Sechseck: Flächeninhalt (mathe-lexikon.at)
dann hast du schon mal die Grundfläche des Sechsecks
Prisma + 2 Pyramiden
hol dir die Formel für die Fläche eines Sechsecks : AS
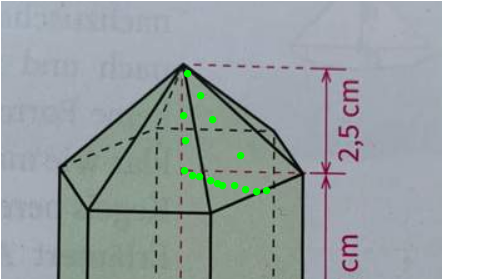
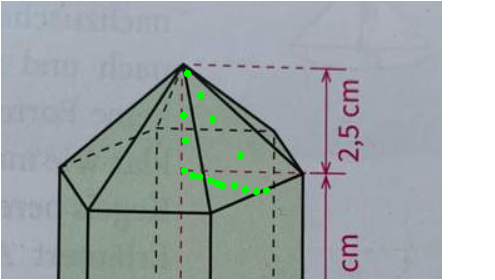
AS = Sechs gleichseitige Dreiecke mit Höhe H (viele grüne Punkte)
Die Höhe ist 3² = h² + (3/2)²
Dann ist V
= 2 * 1/3 * AS * 2.5 + AS * 5
.
.
und für O braucht man noch die Höhe der Dreiecksflächen HD
HD² = 1.5² + H²
.
Dann ist O =
2* 6 * 3 * HD / 2
+
6 * 3 * 5
https://www.mathelounge.de/515881/volumen-eines-kristalls-berechnen-geometrie
kommen dir die Maße nicht bekannt vor ;)
Hallo Ami,
hast du denn eine Idee, wie man das Volumen eines solchen Körpers berechnen kann, der sich aus mehreren Teilkörpern (hier ja laut Aufgabenstellung ein Prisma und zwei Pyramiden) zusammensetzt?
Vielen lieben Dank für deine Mühe!