Vielfachheit?
Hallo , kann mir jmd. helfen und mir erklären wie man die vielfachheit bei der ersten Aufgabe erkennt?(Nur die Vielfachheit) Danke !

4 Antworten
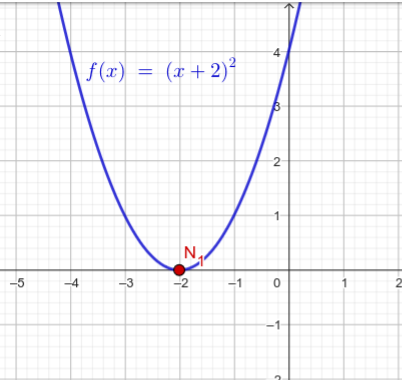
Das Quadrat (hoch 2) sagt aus, dass die Vielfachheit der Nullstelle 2 ist. Am Graphen erkennt man das daran, dass der Graph die x-Achse an der Stelle nur berührt, aber nicht schneidet.
Skizze zu a)

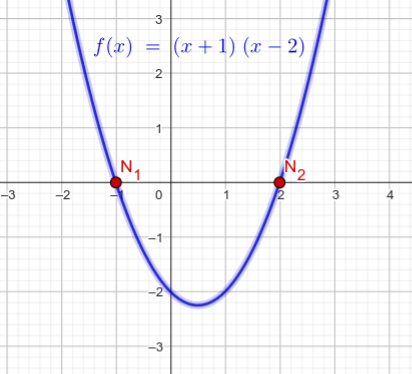
Bei Aufgabe b) hat jede der beiden Nullstellen nur eine 1 im Exponenten (die dann auch gar nicht hingeschrieben zu werden braucht) und daher ist die Vielfachheit jeder der beiden Nullstelle 1 und der Graph schneidet die x-Achse.
Skizze zu b)

Was soll das jetzt heißen?
In meiner Antwort steht, dass x = - 2 in Aufgabe a) eine doppelte Nullstelle ist, während in Aufgabe b) die Nullstellen x = -1 und x = 2 jeweils eine einfache Nullstelle sind.
Warum ist das eine einfache? Weil das sind ja 2 NST mich hoch 1? Also (x+1)(x-2)
Aus den Linearfaktoren
1/2*(x² - 2x - 8) = 1/2*(x-4)*(x+2)
ergeben sich die Nullstellen 4 und -2. Da sie verschieden sind, ist die Vielfachheit von beiden 1.
Beim ersten Beispiel kommt die Nullstelle x = -2 zwei Mal vor. Das erkennst du daran dass beim Faktor für diese Nullstelle (also (x + 2)²) eben ein Quadrat steht. Dieses kannst du auch als (x + 2)(x + 2) schreiben, du siehst dass die -2 zwei Mal erscheint. Beim zweiten Beispiel gibt es zwei unterschiedliche Nullstellen. Im Graphen erkennst du die doppelte Nullstelle daran dass bei der Nullstelle die x-Achse nicht durchkreuzt, sondern nur berührt wird.

man schreibt ohne Exponenten ² alles mit Faktoren hin
(x+2)(x+2) .......................und (x+1)(x-2)
kommt ein Faktor ( vorne (x+2) ) zweimal vor , besteht eine doppelte Vielfachheit
.
(x+5)³ * (x-1) * (x+8)²
drei NST
-5 dreifache , +1 einfache , -8 zweifache

Achsoo, also ist die 1 dann eine doppelte und die zweite 2 einfache NST?