Tangenten berechnen?
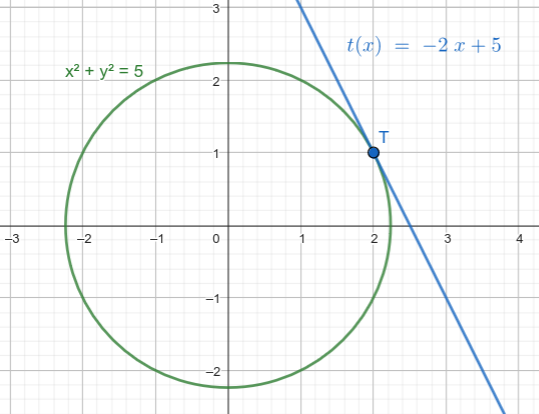
Berechne die Tangentengleichunge an das punkt (2/1) von der funktion des Kreises x^2+y^2=5
Die erste Tangente habe ich gerechnet die ist t(x)=-2x+5 aber wie kann ich die zweite tangente rechnen?
Es ist gemeint das zwei y konnen x=2 machenDa dort war der punkt P(2/y) gegeben
2 Antworten
Die erste Tangente habe ich gerechnet die ist t(x)=-2x+5 aber wie kann ich die zweite tangente rechnen?
... welche zweite?

Nachtrag nach Kommentar: Dann war Deine Aufgabenstellung ja wohl eine andere als Du in der Frage formuliert hattest und die zweite Tangente ist in diesem Fall die an der x-Achse gespiegelte Gerade.

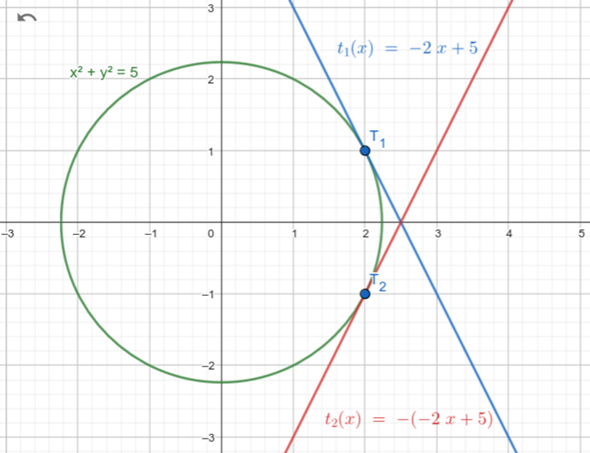
Ich habe es anders gemacht. Ich habe die Punkt P(2/-1) genommen und habe gerechnet das t(x)=-2x+3 war da die steigung in punk 2 bleibt -2 oder?
Nun ja - es ist ja vorstellbar, dass in anderen Unteraufgaben der gegebene Punkt nicht auf, sondern außerhalb der Kreislinie liegt und dann gäbe es zwei Tangenten.
Es ist gemeint das zwei y konnen x=2 machen
Dann hast Du aber Deine Frage falsch gestellt. Das kann niemand riechen, dass Du eigentlich eine andere Aufgabenstellung hast. Poste die komplette Aufgabe und Du bekommst eine korrekte Antwort auf die Aufgabe. So bekommst Du nur eine Antwort auf Deine Frage.
(2;1) ist ein Punkt des Kreises. Ein Kreis hat in einem Punkt nur eine Tangente.
Ich weiß es auch nich aber in der Übung war geschrieben die Tangente Gleichungen und ich habe gedacht das das war plural?