Tangentengleichung?
Gegeben ist eine auf R definierte Funktionenschar /, mit/_(x)= a-x.a> 0
ta ist die Tangente an den Graphen von fa im Punkt (1|f.(1)).
a) Zeigen Sie, dass ta(x) = 2a -x-a eine Gleichung von ta ist
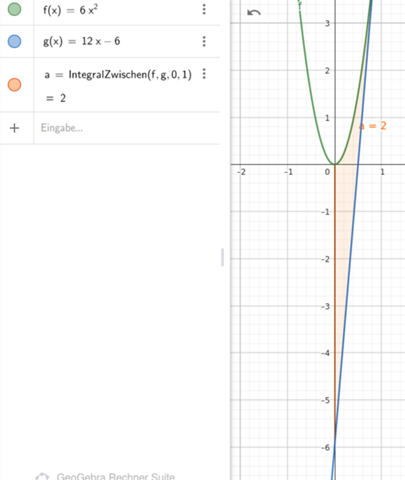
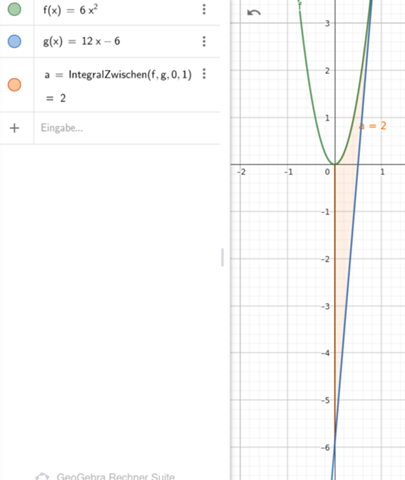
b) Der Graph von fa und die Tangente ta schließen mit der y-Achse eine flache ein.
Bestimmen Sie den Wert des Parameters a so, dass der Inhalt der Flache den Wert 2 hat.
Wie kann man das lösen ich check das nicht brauche bitte eure Hilfe
wie lautet die Funktion genau? f(x)=a-x macht keinen Sinn
fa(x)=a*x^2
1 Antwort
f(x)=ax²
f'(x)=2ax
Berührpunkt der Tangenten (1|f(1))
x=1
y=f(1)=a*1²=a
Steigung m der Tangenten m=f'(1)=2a*1=2a
Tangente ta(x)=mx+c
y für ta(x) sowie x und m einsetzen und dann c ausrechnen:
a = 2a*1+c
daraus c=-a
die Tangente lautet dann ta(x)=2a*x-a
b)
Parabel verläuft oberhalb
Grenzen der Fläche sind x=0 (y-Achse) und x=1 (Berührpunkt)
a=6