stärkste krümmung kurve?
Hallo :)
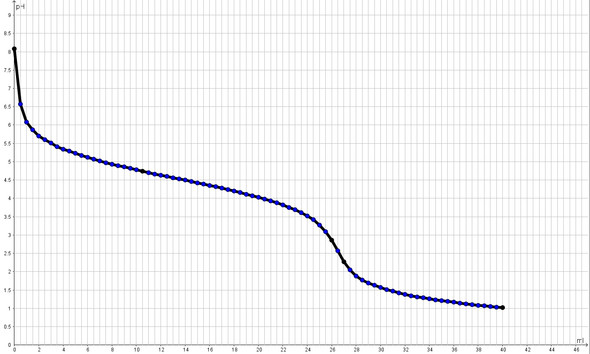
Ich hab eine Linie auf Millimeterpapier gezeichnet, bestehens aus 40 Werten. Wie komme ich auf die beiden Punkte mit der stärksten Krümmung? (Nicht geschätzt sondern genau).
Wobei es ist egal ob es zeichnerisch oder rechnerisch gelöst wird. Mit meinem Programm kann ich zwar den graph zeichnen (Punkte und danach einen Strich durch) allerdings ist es unmöglich es zu berechnen. Wenn ich eine Tangente an einer bestimmten stelle zeichnen möchte, kommt ein waagrechter strich, da es noch immer als punkt und nicht als kurve angesehen wird (Geogebra). Die Punkte sollten ca. bei 25 und 28 liegen.
Danke :)
LG
4 Antworten
Da Dir die Daten ja digital vorliegen, kannst Du die Krümmungen (z.B. mit EXCEL oder OpenOffice) wie folgt berechnen:
Jeweils drei benachbarte Punkte (n-1), (n) und (n+1) bilden ein Dreieck. Die Seite c ist die Gerade zwischen (n-1) und (n+1), b die zwischen (n-1) und (n) und a die zwischen (n) und (n+1). Die Höhe Hc vom Punkt (n) auf die Seite c ist ein Maß für die Krümmung der Kurve im Punkt (n).
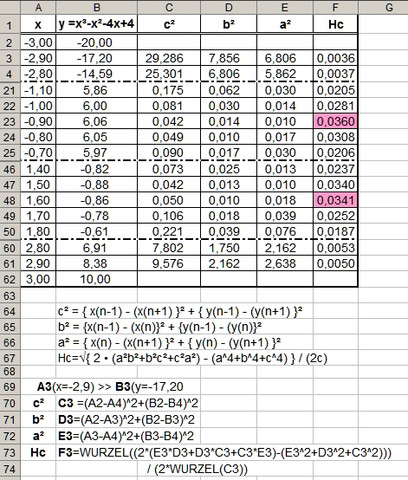
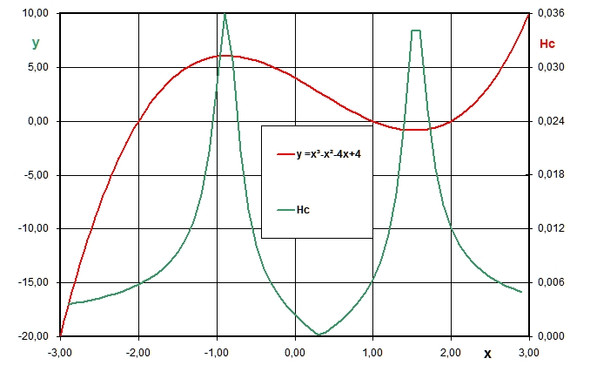
Ich habe das mal für eine Funktion y = x³ -x² -4x +4 (Nullstellen bei -2; 1 und 2) für |x| ≤ 3 berechnet (Bild Tabelle) und Hc gezeichnet (Bild Diagramm).
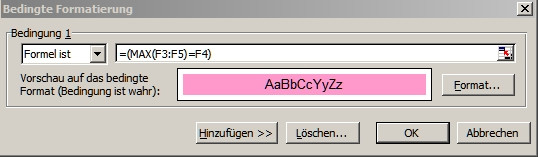
Das Bild Format zeigt (beispielhaft für den Wert in F4) die bedingte Formatierung zum Markieren der Maxima.
Ein Problem könnte sich durch Meßungenauigkeiten ergeben. Eventuell mußt Du die Kurve vorher noch glätten.
Natürlich kannst Du die Krümmung aus den Koordinaten berechnen. Du brauchst dazu genau drei beieinander liegende Punkte. Du berechnest zuerst zweimal die erste Ableitung, in dem Du die Differenzenquotienten bildest. Mit den beiden gewonnene Differenzenquotient bildest Du dann den Differenzenquotienten der Differenzenquotienten.
Das allerbeste ist aber, wenn Du Dir eine Fertigformel für den Differenzenquotienten der Differenzenquotienten selbst herleitest. Da brauchst Du dann nur noch drei Koordinaten eintragen und hast auf einen Schlag Deine gesuchte Krümmung.
Vielleicht noch die Anmerkung, dass wir mit "Krümmung" immer die zweite Ableitung meinen. Streng genommen müsste man auch noch nach einem lokalen Krümmungsradius fragen. Das ist jedoch was anderes und gleichzeitig spielt da auch noch die Achs-Skalierung hinein.
Und genau da liegt ja das Problem,.. ich kanns nicht ableiten weil ich keine Funktion hab... Ich hab nur gemessene werte (an stelle 1 wert 8.2, an stelle 1.5 wert,... usw)
daran scheitere ich ja,.. ich habe keine funktion sondern nur gemessene werte mit denen ich nix machen kann... :/
oder kann man irgendwie von mehreren punkten auf eine funktion kommen?
Oder hab ich das falsch verstanden?
Schon mal mit dem Verfahren nach Newton-Gregory versucht?
da du ja die y-Werte aller Punkte kennst, berechne doch ganz simpel die Differenz benachbarter Punkte, also das Delta-y. das ist genau bei den beiden gesuchten Punkten betragsmäßig maximal.
hm - guter Einwand. De fakto bildet mein obiger Vorschlag ja nur die Steigung ab (= 1. Ableitung), aber wenn man das noch ein zweites mal analog anwendet, dann hätte man die 2.Ableitung. Dann müsste man nur noch überlegen, was "stärkste Krümmung" bedeuten mag - eine Nullstelle der 2.Ableitung führt ja "nur" zum Wendepunkt (der nicht unbedingt die stärkste Krümmung haben muss).
Aber wäre dass dann nicht ca beim punkt 26.5? da wäre dann ungefähr der wendepunkt oder?