Sachzusammenhänge bei funktionen?
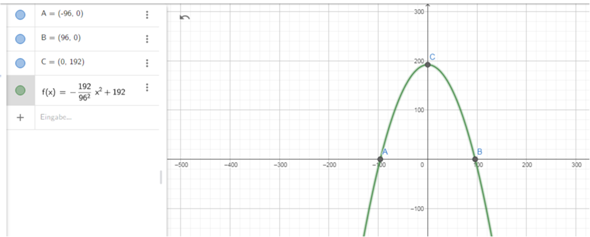
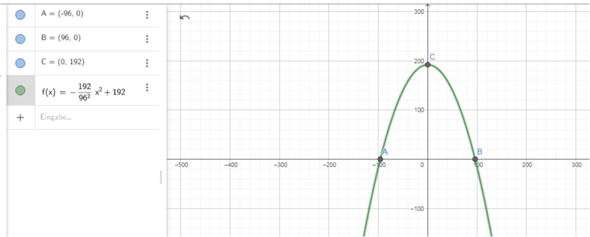
Der Gateway Arch ist das Wahrzeichen von St. Louis (USA) und mit 192 m das höchste Bauwerk der Stadt. Der Bogen hat die Form einer Parabel. Die Spannweite des Bogens beträgt ebenfalls 192 m.
Bestimmen Sie eine quadratische Funktion, die den Gateway Arch beschreibt und stellen Sie Ihr Ergebnis in Normalform dar. Kann Mir jmd sagen wie genau ich es rechnen soll evt mit Lösung.
2 Antworten
Wenn Du den Scheitelpunkt des Bogens auf die y-Achse legst, dann geht der Bogen von x=-192/2 bis x=+192/2, also von -96 bis +96.
Das sind die Nullstellen Deiner quadr. Funktion. Da Du diese kennst nutzt Du zur Ermittlung der Funktionsgleichung die Nullstellenform f(x)=a*(x minus Nullstelle1)*(x minus Nullstelle2), indem Du dort die Nullstellen einsetzt und zudem den Scheitelpunkt (0|192) und das dann nach a umstellst.
Letztendlich dann nur noch die Nullstellenform ausmultiplizieren um an die gefragte Normalform (f(x)=ax²+bx+c) zu kommen.
Das sind die Punkte
Ansatz
Den Scheitelpunkt (0/192) auf die y - Achse legen
f(x) = a*x² + 192
Einen der beiden Punkte einsetzen
0 = a*96² + 192
-192/96² = a
Parabel ist
f(x) = -192/96² * x² + 192
Das ist schon die Normalform ( -192/96² evtl in gerundete Dezimalschreibweise bringen )
.
.
.