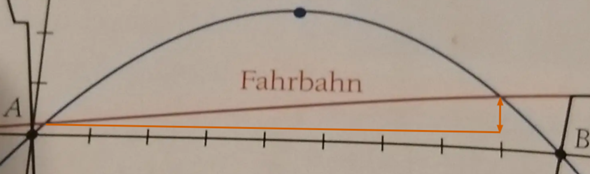
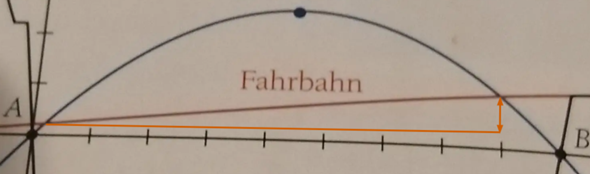
Quadratische Funktion Anwendungsaufgabe Brückenbogen?
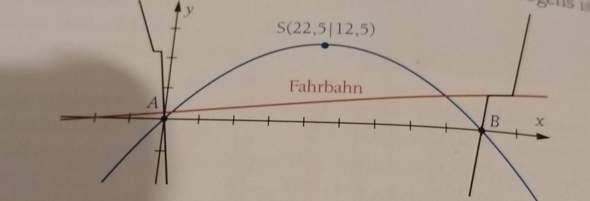
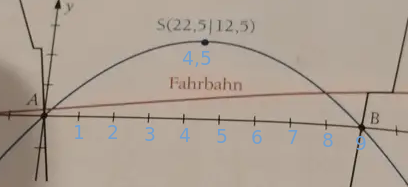
Gegebene Funktion: g(x)=0.1x+1 und Scheitelpunkt S(22,5|12,5)
Gesucht:
1)Funktionsgleichung der Parabel
2)Spannweite von Punkt A bis B
3)Höhenunterschied der Straße innerhalb des Brückenbogens überwindet
So mein Ansatz wäre, dass man erstmal die Scheitelpunktform in die Allgemeine Form bringt. Danach kann man mithilfe der PQ-Formel die Nullstellen von a und B berechnen und hätte dann die Spannweite von Punkt A bis B. Zeitgleich lösen wir auch die Aufgabe 1.
Wie man die 3) berechnet keine Ahnung.
Die Scheitelpunktform sieht so aus: f(x)=a*(x-22,5)²+12,5 a ist 1 glaube ich, warum weiß ich auch nicht genau.
Das müsste ich dann in die Allgemeinform bringen.
Funktion lautet: x²+45x+50,625+12,25
x²+45x+62,650? Hilfe:D
1 Antwort
...a ist 1 glaube ich, warum weiß ich auch nicht genau.
Die Parabel ist nach unten geöffnet. Das bedeutet, dass a negativ sein muss. +1 kann es dann schon mal nicht sein (und -1 ist es auch nicht).
.
Auf der Skizze sieht man, dass (0|0) ein Punkt der Parabel ist. Setz diesen ein und bestimme a:
f(x) = a(x - 22,5)² + 12,5
x = 0 und f(0) = 0
0 = a(0 - 22,5)² + 12,5 |-12,5
-12,5 = (-22,5)²•a
-12,5 = 506,25a |:506,25
-12,5/506,25 = a
kann man ausrechnen, ≈ -0,02469...
Man kann es als Bruch scheiben (mit 100 erweitern):
-1250/50625 und kürzen (mit 625), ergibt -2/81
f(x) = -2/81•(x - 22,5)² + 12,5
.
Für b) kann man die Nullstellen ausrechnen. Muss man aber nicht.
Der Scheitelpunkt (22,5|12,5) (vermutlich sind das Meterangaben, also 22,5m und 12,5m) liegt mittig zwischen den Nullstellen. Wenn die Mitte 22,5 m ist, was ist das Ganze?
Oder:
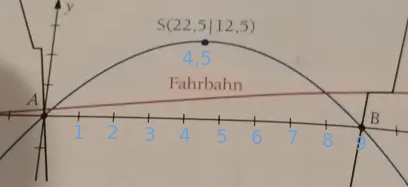
Der Scheitelpunkt liegt bei 4,5 "Strichen". Wenn das 22,5 m sind, wie groß ist ein "Strich"? Und wie groß sind dann 9 "Striche" (Nullstelle B)?
.
Schnittpunkte Straße - Brückenbogen berechnen. y-Werte dr Schnittpunkte betrachten.