Wie berechne ich diese Matheaufgabe (Parabeln)?
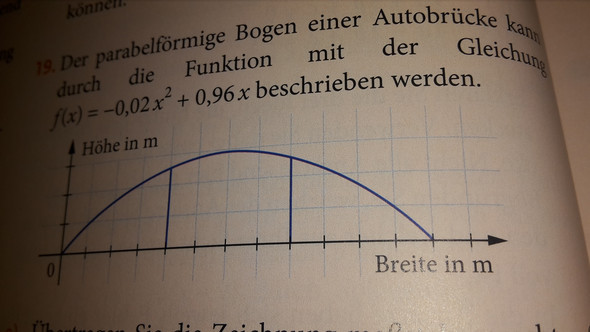
Der parabelförmige Bogen einer Autobahnbrücke kann durch die Funktion f(x)= -0,02x^2+0,96x beschrieben werden.
Berechnen sie die Spannweite des Brückenbogens.
-> Dafür habe ich die Nullstellen ausgerechnen. Diese liegen bei mir bei x=0 und x=-1. Kann das sein? Wie komme ich nun von den Nullstellen aus auf die Spannweite (Die Spannweite liegt zwischen den Nullstellen auf der x-Achse)
4 Antworten
zuerst musst du f(x)=0 setzen:
0=-0,02x²+0,96x
dann die -0,02 vor dem x² wegmachen indem du eine beidseitige divison durch -0,02 machst. dann hast du nur noch 0=x²+0,96x. das kannst du in die pq-Formel einsetzen (so mache ich das immer): p=0,96; q=0
x1/2=-0,96/2 +/- wurzel aus (0,96/2)²-0
x=-0,48+/- wurzel aus 0,2304
x=-0,48+/-0,48
x1=0 x2=-0,96
das wären die nullstellen und auf die spannweite kommst du indem du einfach die entfernung von der nullstelle x1 zu x2 berechnest also in diesem fall 0,96m
Wenn man schon die pq-Formel nutzen möchte, was in meinen Augen nicht der einfachste Weg ist, sollte man sich nicht schon am Anfang verrechnen.
0=-0,02x²+0,96x
dann die -0,02 vor dem x² wegmachen indem du eine beidseitige divison durch -0,02 machst. dann hast du nur noch 0=x²+0,96x.
Warum teilst du nicht auch 0,96x durch -0,02?
0=-0,02x²+0,96x ∣:(-0,02)
0 = x² - 48x
p = -48
x1,2 = -p/2 ± √(p/2)²
x1,2 = +24 ± √576
x1,2 = 24 ± 24
Wenn ichs im Kopf rechne sollten die Nullstellen x=0 und x=48 sein.
Hallo cooleDame,
du musst die -0,02 vor dem x² noch wegbekommen. Du kannst die p-q Formel so noch nicht anwenden.
Grüße
der Abstand der beiden Nullstellen zueinander ist die Spannweite;
und die Nullstellen kannst du doch selbst durch einsetzen überprüfen.
ein Abstand ist der Betrag eines Vektors, damit ist er immer positiv und angenommen deine Nullstellen stimmen, dann ist er schlicht +1
Dann wäre doch der Abstand aber -1. und das macht doch keinen Sinn?