Quader Kiste ohne Deckel mit maximalem Volumen?
Moin,
also die Kiste soll halt ne Oberfläche von 27 cm^2 haben und dabei maximales Volumen.
habe ich irgendeinen Fehler bei meiner Rechnung, da zum Schluss jetzt kein sinnvoller Punkt für ab rauskommt.
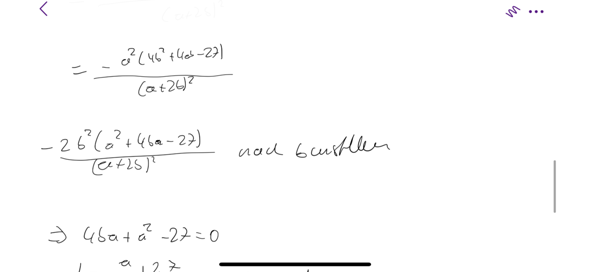
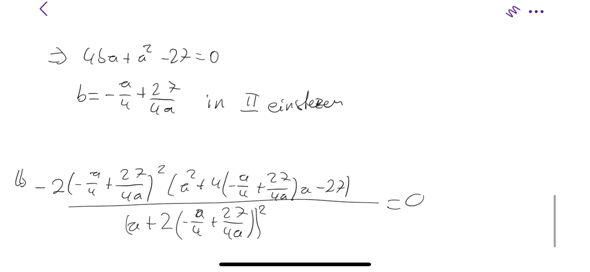
6 Antworten
ich gehe mal davon aus, dass das ideale verhältnis zwischen volumen und oberfläche, sofern der quader vorgegeben ist, beim würfel erreicht wird. der würfel ist ein quader mit gleichen seitenlängen in allen drei dimensionen.
wir haben also die vorgabe, 27 cm² gesamtoberfläche.
da so ein würfel 6 flächen hat, hat jede fläche 27/6 also 4,5 cm² macht etwa2,1 cm kantenlänge. heraus kommen etwa 9,55 cm³ volumen.
machen wir einfach mal den versuch, des baus einer "länglichen kiste mit den stirnseiten von 1 x 1 cm.
dann bleiben uns für die verkleidung der seiten noch 25 cm² über. der unfang unserer stirnflächen ist 4 cm. das bedeutet, die länge unserer kiste beträgt 6,25 cm.
6,25 x 1 x 1 cm sind 6,25 cm²
hast du immer noch nicht genug? dann rechnen wir mal mit einer länglichen kiste mit den stirnseitenmaßen 2 x 1 cm
ziehen wir diese beiden stirnflächen von den 27 cm² ab, erhalten wir 23 cm² an restfläche für die seitenteile.
der umfang eines rechteckes 2 x 1 cm beträgt 6 cm. also können wir mit der vorgegebenen fläche noch eine kiste von 3,88 cm länge bauen. so kommen wir dann 2 x 1 x 3,88 cm auf 7,66 cm³
lg, anna
Ich habe Deine Bezeichnungen übernommen für Länge, Breite und Höhe.
V(a, b) = a * b * (27 - 2ab) / (2b + a)
∂V / ∂a = -2 * b² * (a² + 4 * a * b - 27) / (a + 2 * b)²
∂V / ∂b = a² * (-4 * a * b - 4 * b² + 27) / (a + 2 * b)²
gleich Nullsetzen und vereinfachen führt zu:
(1) 0 = a² + 4 * a * b - 27
(2) 0 = -4 * a * b - 4 * b² + 27
(1) b = (-a² + 27) / 4 * a
(1) in (2) 0 = -4 * a * [(-a² + 27) / 4 * a] - 4 * [(-a² + 27) / 4 * a]² + 27
Diese Gleichung sieht etwas einfacher aus, da ich vorher schon gekürzt habe und führt zu
a = 3
b = 3 / 2
...
Tipp: Aus (1)+(2) folgt sofort a²=4b². Damit muss man nur noch 0=a²+2a²–27 lösen.
Hallo, was hälts Du von diesem Ansatz:
Ein Würfel ist der Quader, der bei minimaler Oberfläche das maximale Volumen hat. Das muß auch für einen halbierten Würfel gelten, bei dem man die Schnittflächen nicht berücksichtigt (wie in der Aufgabe).
Wir suchen also einen Würfel mit der Oberfläche 2x27cm².
Kantenlänge a = √(54cm²/6) = 3cm
Ergebnis: Kiste 3x3x1,5 cm³
Das ist auf jeden Fall der kürzeste Lösungsweg.
Er setzt die Kenntnis voraus, dass der Würfel der Quader ist, der bei minimaler Oberfläche das maximaler Volumen hat und dass das auch gilt, wenn der Würfel halbiert wird.
Es gibt Extremwertaufgaben, wo die Lösung gerade in dieser oder ähnlicher Erkenntnisse besteht. Darf man das voraussetzen?
Ob der Aufgabensteller diese Prämissen akzeptiert oder belegt haben möchte, dass z.B. die Grundfläche ein Quadrat sein muss, weiß ich nicht. Das wird vom Lehrer/Prof. abhängen. Die Aufgabenstellung gibt das nicht her.
Wenn man durch Rechnung belegen kann, also hier durch Null setzen der partiellen Ableitungen, ist man zumindest auf der sicheren Seite, wobei der Vorschlag von ralphdieter, die Höhe b zu eliminieren, die Rechnung mit der Erkenntnis a = c abkürzt.
Du hast Dich bei den Richtungsableitungen verhauen. Ich komme auf die Zähler
∂f/∂a: (27b–4ab²)(a+2b)–(27ab–2a²b²)·1 = 54b²–2a²b²–8ab³
⇒ 27–a²−4ab=0
∂f/∂b: (27a–4a²b)(a+2b)–(27ab–2a²b²)·2 = 27a²–4a³b–4a²b²
⇒ 27–4ab–4b²=0
Daraus bekommst Du mit etwas Mühe a=3 und b=3/2.
Leichter wäre es gewesen, statt c die Höhe b zu eliminieren. Dann sieht man die Symmetrie in V(a,c) und kann sofort a=c folgern. Das vereinfacht die weitere Rechnung gewaltig.
Die Grundfläche der Kiste ist ein Rechteck.
Welche Fläche eines Rechtecks hat den kleinsten Umfang?
Ein QUADRAT mit der Seitenlänge a
Mit diesem Wissen ist das Volumen V = a² • h mit der Höhe h und die Oberfläche O = 27 = a² + 4a•h
Hallo,
da ein Quader bis zu drei unterschiedliche Maße für Länge, Breite und Höhe besitzt, kannst Du diese Aufgabe nicht auf herkömmliche Art lösen. Für Schüler wird daher noch die Bedingung mitgegeben, daß es sich um einen Quader mit quadratischer Grundfläche handelt.
Fehlt diese Angabe, mußt Du mit dem Lagrange-Multiplikator und partiellen Ableitungen an die Sache herangehen, was aber kein Schulstoff mehr ist.
Zu Deiner Information: x=y=3, z=1,5 ergibt das maximale Volumen.
Herzliche Grüße,
Willy
Ne ist auch Uni 😅
aber das habe ich doch auch soweit gemacht oder nicht
Hallo, was haltet ihr von diesem Ansatz:
Ein Würfel ist der Quader, der bei minimaler Oberfläche das maximale Volumen hat. Das muß auch für einen halbierten Würfel gelten, bei dem man die Schnittflächen nicht berücksichtigt (wie in der Aufgabe).
Wir suchen also einen Würfel mit der Oberfläche 2x27cm².
Kantenlänge a = √(54cm²/6) = 3cm
Ergebnis: Kiste 3x3x1,5 cm³
Danke für Deine Mühe!
Leider hattest Du überlesen, dass die Kiste keinen Deckel haben soll. (:-(((