PQ-Formel Probe?
Hallo,
Ich schreibe eine Arbeit über die PQ-Formel und brauche Hilfe mit der Probe. Soweit ich es weiß und laut dem Internet soll bei der Probe 0 rauskommen, aber bei dieser Aufgabe kommt nicht 0 raus, auch nicht in den Lösungen im Buch. Könnt ihr mir bitte weiterhelfen?
x²= 1/18 - 1/6x |-(-1/6x)
x²+1/6x=1/18 |-1/18
x²-1/6x-1/18=0
x½= -1/12 + √(-1/12)²+1/18
x½= -1/12+ 1/4 (1/4 = 3/12)
x1= -1/12+3/12=1/6
x2= -1/12-3/12=-1/3. Also: L= {-1/3|1/6}
P: (-1/3)²=1/9. ✓
(weil: 1/18-1/6×(-1/3)=1/9)
P: 1/6²= 1/36✓
Also, was hat das jetzt zu bedeuten? Muss es 0 sein?
4 Antworten
P: (-1/3)²=1/9.
Soll das deine Probe sein?
Die ist schonmal falsch.
Du musst deine errechneten x in die volle gleichung einsetzen:
Also x² = 1/8 - 1/6 x
Und wenn beide seiten gleich sind. Dann ist der wert korrekt.
Die Sache mit der 0 kommt daher weil die gleichungen normalerweise in der Form:
y = x² + px +q
Stehen.
Im endeffekt das hier:
x²-1/6x-1/18=0
Und wenn du es in dieser gleichung einsetzt müsste es 0 ergeben.
Und hier ist dir noch ein fehler unterlaufen.
x²+1/6x=1/18 |-1/18
Hier haste + 1/6 stehen.
Aber nen schritt weiter nachdem du die 1/18 abgezogen hast. Steht da -1/6x
x²-1/6x-1/18=0
Schau.
Die Korrekt umgestellte gleichung lautet:
y = x² +1/6x -1/18
x½= -1/12 + √(-1/12)²+1/18
Und hier haste die werte auch noch falsch eingesetzt.
Wenn du P mit -1/6 genommen hättest Müsste da am anfang 1/12 stehen und nicht -1/12 weil es - p/2 heisst. Und die Minus sich beide vernichten.
Wenn du P mit 1/16 genommen hättest müsste unter der Wurzel 1/12 stehen. (Wobei das hier aufgrund des Quadrates keinen unterschied macht.)
Rechne das am besten nochmal ganz von vorne.
Guck nochmal durch. Meistens ist es ein Vorzeichenfehler, der sich irgendwo unterwegs eingeschlichen hat. Oder ein Bruch wurde falsch gekürzt. Ich vermute mal, dass du mit p/2 anstatt mit -p/2 gearbeitet hast. Aber es muss nicht der einzige Fehler sein.
Auch ist 6² nicht 16!
Ich habe mich vertippt, ich meinte 1/6²=1/36. 🥲 Aber ja, genau das steht im Buch...
erstens : Vorzeichenfehler

p = -1/6 ..................-p/2 also +1/12
.
probe geht einfacher so

-1/3 mal 1/6 muss -1/18 sein ..................stimmt hier
und
-1/3 plus 1/6 muss PLUS 1/6 sein
-2/6 + 1/6 = -1/6.................falsch , Lösungsmenge falsch
hier reicht es dann die Vorzeichen von x1 und x2 zu tauschen
.
.
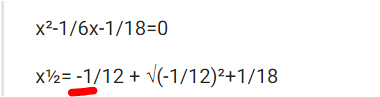
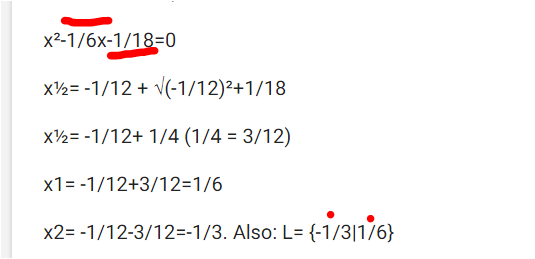
Probe mit 1/6:
(1/6)²=1/18-1/6*1/6
1/36=2/36-1/36
1/36=1/36 - passt.
Wenn es mal nicht passen sollte, ist entweder das Ergebnis falsch, oder wie hier bei Dir die Probe!
(in der dritten Zeile hast Du Dich verschrieben [Vorzeichenfehler beim p] - das Einsetzen in die Formel stimmt aber wieder)