Nullstellen von cosinus?

Lose die Gleichung f(x)=2cos(3x-6)+1

Ich habe 3x-6=z gesezt und habe heraus gefunden das z=2pi/3 ist. Dann habe ich x1 herausgefunden die 1.0314 ist. Die periode hier ist 2pi/3 und ich habe zu diese wert diese periode addiert und die losungen gefunden. Die Losung ist im intervall 0 bis 2pi eingeschrankt

Answer 1

[PWolff]

z = 2/3 pi ist tatsächlich eine Lösung von cos(z) = -1/2.

Wegen

cos(x) = cos(-x) = cos(2 pi - x)

ist auch

z = 2 pi - 2/3 pi = 4/3 pi

eine Lösung von cos(z) = -1/2.

Die Periode ist, wie du sagtest, 2/3 pi.

Wieso ist die Lösung auf das Intervall [0, 2 pi) eingeschränkt? Steht das so in der Aufgabenstellung?

Bezieht sich das Intervall [0, 2 pi) auf x oder auf z?

Answer 2

[gauss58]

0 = 2 * cos(3x - 6) + 1

cos(3x - 6) = -1 / 2

3x - 6 = (2 / 3) * π + 2 * n * π ∨ 3x - 6 = 2 * π - (2 / 3) * π + 2 * n * π ; n ϵ Z

3x - 6 = (2 / 3) * π + 2 * n * π ∨ 3x - 6 = (4 / 3) * π + 2 * n * π

x = (2 / 9) * π + (2 / 3) * n * π + 2 ∨ x = (4 / 9) * π + (2 / 3) * n * π + 2

Im Intervall [0 ; 2π] :

L = {0,603... ; 1,302... ; 2,698... ; 3,396... ; 4,792... ; 5,490... }

Answer 3

[Halbrecht]

mit x = 1.0314 keine Nullstelle

Comments

[Waves08]

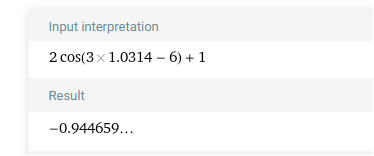
ja ja ich habbe eine fehler gemacht statt -6 zu rechnen habe ich -1 gemacht