Mathe Differenzialrechnung Steigung in einem Punkt?
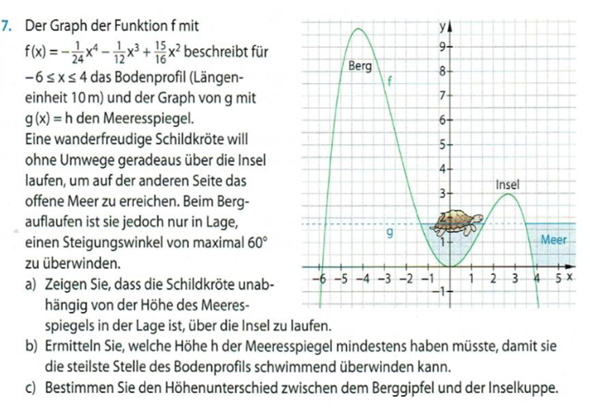
Ich benötige hilfe bei a). Könnte mir das wer sagen mit welcher Formel ich da rechnen muss? Ausrechnen möchte ich es selber.
b) und c) habe ich bereits gelößt.
5 Antworten
Die Funktion für die Steigung lautet:
f(x) = -1/6 x^3 - 1/4 x^2 + 15/8 x
Diese müssen wir diskutieren und das Maximum im Intervall 0 bis etwa 3 finden:

Damit können wir die Extrempunkte suchen:

Uns interessiert aber nur das Extremum bei 1,5, denn -2,5 liegt außerhalb des Intervalls:

Die maximale Steigung beim Überklettern der Insel beträgt also 1,69.
Steigung von 60° = tan 60° = 1,73
Ergebnis: da im Intervall 0 bis 3 die maximale Steigung 1,68 beträgt, die Schildkröte aber bis zu 1,73 bewältigen könnte, kann sie die Insel unabhängig vom Wasserstand erfolgreich überklettern.



Weil wir den x-Wert nicht in die Ursprungsfunktion (Ortsfunktion) eingesetzt haben (dann wäre der y-Wert die Höhe), sondern in die Funktion der Ableitung, die die Steigung angibt. Der y-Wert der Steigungsfunktion ergibt die Steigung im Punkt x.
Ich habe die erste Ableitung der Ursprungsfunktion ebenfalls f(x) genannt, weil ich praktisch neu nur mit der Steigung angefangen habe und mein Tool, nur f(x) und nicht f'(x) als Eingabe annimmt.
Man hätte meine Rechnung auch mit f' anfangen können und alle weiteren Ableitungen davon einen hochsetzen können.
Die Steigung wird mit der ersten Ableitung ausgedrückt:
f'(x) = -1/6 x^3 - 1/4 x^2 + 15/8 x
Für den Bereich 0 ≤ x ≤ 2,5 musst du nun das Maximum von f' finden. Dazu führst du eine Kurvendiskussion für f'(x) durch
Dazu musst du f' nochmal ableiten und dann f'' = 0 setzen. Das muss einen Hochpunkt (= maximale Steigung) ergeben, denn an den beiden Rändern des Intervalls ist die Steigung = 0
Dann musst du noch den Winkel von 60° in eine Steigung m umrechnen und das geht mit dem tangens.
Zum Schluss musst du feststellen, dass das Maximum von f' kleiner ist als m. Wenn das gelingt, ist der geforderte Nachweis erbracht.
Setze ich dei zweite Ableitung gleich Null, erhalte ich die Wendepunkte -5/2 und 3/2.
Wenn ich tan(1,5) nehme, erhalte ich 14,1.
Bei tan^-1(1,5)=0,98
Und tan^-1(60)= 1,554
Ist das denn Richtig mit der Steigung von 0,98 und 1,55?
a) das Maximum der Steigung f´(x)=m ermitteln
2 mal ableiten
f(x)=-1/24*x³-1/12*x³+15/16*x²
f´(x)=m=-1/6*x³-1/4*x²+15/8*x
f´´(x)=0=-1/2*x²-1/2*x+15/8 Nullstellen mit meinem Graphikrechner (GTR,Casio)
x1=m1=-2,5 und x2=m2=1,5
Winkel zwischen der Tangente und der x-Achse tan(a)=Gk/Ak=m
(a)=arctan(m)=arctan(1,5)=56,31°<60° also schafft die Schildkröte auch die steilste Stelle.
Infos,Kurvendiskussion,vergrößern und/oder herunterladen


tan^-1(1,5)=0,98. Ich erhalte da keinen Winkel, sondern nur 0,98.
Rechner auf Grad einstellen (oben steht DEG)
wenn da rad (Radiant) steht,dann rechnet der in Bogenmaß
Eingabefolge bei meinem Casio
1) 1,5 eingeben
2) Taste "SHIFTt" drücken und dann Taste "tan"
Hinweis:Die Taste "tan" ist doppelt belegt
Mit Taste "SHIFT" wir die Funktion "tan^(1)" aufgerufen.
(a)=arctan(1,5)=56,309..
tan(56,309)=1,5
Die erste Ableitung ist die Steigung.
Wenn man wissen will, wo die Steigung am größten ist, muss man die Nullstelle der zweiten Ableitung ermitteln.
Extrema der Ableitung. Du willst ja die maximale Steigung.
Vielen Dank, aber wenn man einen x Wert in die Funktion f(x) einsätzt, erhält man doch eigentlich den Y Wert, bzw Y Achsen Abschnitt. Warum ist dieser in unserem Fall die Steigung m?