Steigung des Funktionsgraphen im Punkt P?
Hallo,
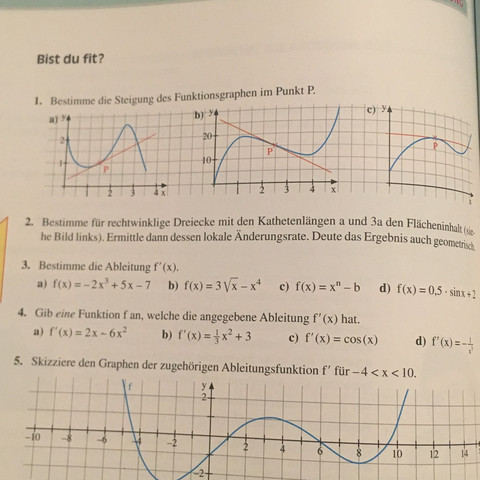
Wir haben ein paar Seiten mit Aufgaben von unserem Lehrer bekommen, um uns auf eine Mathe Klausur vorzubereiten. Jedoch verzweifle ich gerade bereits an Aufgabe 1, bei der man die Steigung im Punkt P (siehe Bild) bestimmen soll. Bei a) weiß ich noch wie dies geht, da man das dort einfach ablesen kann und bei c) ist keine Steigung vorhanden, jedoch muss man bei b) rechnen. Es ist keine Funktionsgleichung gegeben. Seht euch bitte das Bild an, ich würde mich sehr freuen, wenn ihr mir helfen könnten.
Danke
6 Antworten
Steigung durch 2 Punkte "Differenzenquotient" (de)y/(de)x=(y2-y1/(x2-x1)
der Punkt P=P2(1,5/1) wir wählen einen 2.ten Punkt P1(0,5/0,5)
wir haben somit x1=0,5 und y1=0,5 weiter x2=1,5 und y2=1
ergibt Steigung (de)y/(de)x=m=(y2-y1)/(x2-x1)=(1-0,5)/(1,5-0,5)=0,5
Bei einer Geraden ist überall die Steigung m=konstant
3. hier müssen die "Differentationsregeln","elementare Ableitungen" angewendet werden.
siehe Mathe-Formelbuch "Differentationsregeln/elementare Ableitungen"
f(x)=-2*x^3+5*x-7 hier die "Konstantenregel","Summenregel" und "Potenzregel" anwenden.
f´(x)=-2*3*x^2+5*1=-6*x^2+5 beachte -7*x^0=-7*1=-7 das x^0 lässt man weg
b. f(x)=3*Wurzel(x)-x^4=3*x^0,5-x^4
f´(x)=3*0,5*x^(-0,5)-4*x^3=1,5*1/Wurzel(x) - 4*x^3
4. hier die integrationsregeln anwenden,siehe Mathe-Formelbuch "Grundintegrale"
f´(x)=2*x-6*x^2 integriert F(x)=Integral(2*x-6*x^2)*dx
F(x)=2* Int.(x*dx)-6*Int.(x^2*dx) +C
F(x)=2*x^2/2 -6 *x^3/3+C=x^2-3*x^3+C
Grundintegral Integral (x^k *dx)= (x^(k+1))/(k+1) +C
Integral( a*x^k*dx)=a*Integral(x^k*dx
Merke: Ein konstanter Faktor a kann vor das Integralzeichen gezogen werden !
Summenregel Integral(f(x)+g(x)=(Integral (f(x)*dx+Integral(g(x)*dx))+C
Differentationsregeln:
(a*f(x))´=a*f´(x) konstantenregel
(x^k)´=k*x^(k-1) mit x ungleich Null "Potenzregel",elementare Ableitung
Im Punkt P gilt für Tangenten t(x) (Berührgeraden) an P:
f(P)=t(P) ---> hier irrelevant
f'(P)=t'(P) ---> relevant
Gesucht ist also jeweils die Steigung der roten Gerade, welche zeitgleich die Steigung im Punkt P ist, und die ist ja jeweils ablesbar bzw. notfalls errechenbar.
Wie hast du denn bei a die steigung rausgefunden?
Bei b gibt es doch auch eine steigung. Nur das diese negativ ist. Berechnen kannst du die mit einem steigungsdreieck
Und bei c ist die steigung 0
Bei dieser Aufgabe brauchst du keine Funktionsgleichungen, um die Steigung zu berechnen. Denn die Tangenten am Punkt P sind eingezeichnet. Das sind die Roten Geraden im Bild. Sie zeigen die Steigung an diesem Punkt an. Du erhälst die Steigung mit dem Steigungsdreieck
a) Die Steigung ist 1/2 (Wenn du ein Kästchen nach rechts gehst, dann musst du ein halbes Kästchen nach oben gehen)
b) Die Steigung ist -1/2 (Wenn du ein Kästchen nach rechts gehst, dann musst du ein halbes Kästchen nach unten gehen)
c) Die Steigung ist 0 (Wenn du ein Kästchen nach rechts gehst, dann musst du null Kästchen nach oben gehen)
Es müsste -0,5 sein, nicht -5. Das ist ein Druckfehler
b) kann man doch genau so wie a) ablesen
Die Steigung bei b) ist -5, das steht als Lösung im Buch, jedoch weiß ich nicht wie die darauf kommen