Kann mir jemand in Mathe helfen (Zahlenmengen)?
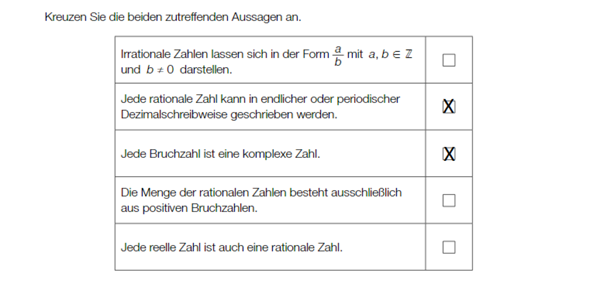
Hey Leute. Ich brauche Hilfe bei dieser Aufgabe. Ich weis zwar dass diese beiden Aussagen korrekt sind, muss aber begründen wieso sie richtig sind und warum die anderen falsch sind. Könnte mir das jemand sagen? Wäre dringend!
Danke im Voraus!
5 Antworten
Also die Begründung für die zweite ist einfach, denn für eine komplexe Zahl gilt ja
Also muss einfach nur b=0 sein und Bruchzahlen sind ja eine Teilmenge der reellen Zahlen, also gilt für jede Bruchzahl auch a aus R.
Bei der ersten dividierst du ja zwei ganze Zahlen, wenn du die rationale Zahl in Dezimaldarstellung umwandeln willst. Geht diese Division irgendwann mit Rest 0 glatt auf, hast du für diese Brüche eine endliche Darstellung als Dezimalzahl. Wird sie periodisch, kannst du es als periodische Dezimalzahl darstellen. Ich gehe mal davon aus, dass einer der beiden Fälle immer auftreten muss, wenn ich zwei natürliche Zahlen dividiere, und es da nicht vorkommen kann, dass eine nicht-periodische und nicht-abbrechende Zahl als Ergebnis entsteht. Aber den Beweis dafür, warum das wirklich so ist, kenne ich dir jetzt auch nicht aus dem Kopf.
Widerlegen der falschen Aussagen:
1) ist die Definition für rationale und nicht für irrationale Zahlen. Gegenbeispiel pi, das ist eine irrationale Zahl und lässt sich nicht als solch einen Bruch darstellen.
4) Rationale Zahlen bestehen aus positiven und negativen Bruchzahlen.
5) Es gilt umgekehrt. Jede rationale ist auch eine reelle Zahl, aber nicht jede reelle auch eine rationale. Gegenbeispiel wieder mit pi, das ist eine reelle Zahl, aber keine rationale, da sie sich wie in 1) angesprochen nicht als Quotient zweier ganzer Zahlen darstellen lässt, was die Bedingung für eine rationale Zahl wäre.
Ich denke mal der saubere Beweis für die b) dürfte sein, dass du ja bei der Division durch eine ganze Zahl a nur eine endliche Anzahl an verschiedenen Resten zwischen 1 und (a-1) haben kannst. Das heißt wenn deine Zahl nicht abbricht mit Rest 0, muss sich, wenn du im Nachkomma-Anteil bist und entsprechend jeweils wieder Nullen nachziehst, irgendwann einer der Reste zwangsläufig wiederholen, der schon mal davor irgendwann da war. Und ab da hast du eben dann deine Periode.
*) jede endliche Dezimalzahl kannst als Bruch schreiben: der Zähler sind alle Ziffern der Zahl (ohne Komma!), der Nenner ist ein 1 mit so vielen Nullen wie Ziffern nach dem Komma →
Beispiel: 0,123456789 = 123456789/100.0000.000
*) jede periodische Dezimalzahl:
Zähler: Die Periode, Nenner: so viele Neuner, wie Periode Stellen hat
Beispiel: 0,123123123... = 123/999
Eine komplexe Zahl besteht aus einem Realteil und einem Imaginärteil → Die reellen Zahlen sind also eine Teilmenge der komplexen Zahlen. Da jede rationale Zahl eine reelle Zahl ist, ist sie auch eine komplexe Zahl.
Beispiel: 3/4 = 3/4 + 0i
Hallöle,
Zu 1. : Richtig wäre, dass man "rationale Zahlen" in der Form aufstellen kann nicht "irrationale"
Zu 2.: Als Beispiel 1/2 = 0.5, 1/3 = 0.33333..
Begründung: man kann jeden Bruch auch als schriftliche Division erfassen und würde dadurch auf die dezimalzahlen stoßen.
Zu 3.: Weil die Rationalen Zahlen Teilmenge der Komplexen Zahlen ist ist jede rationale Zahl eine komplexe Zahl jedoch nicht anders herum.
Zu 4.: Weil die Rationalen Zahlen über die Division von ganzen Zahlen definiert sind ( ausgenommen Nenner 0) muss es auch negative Brüche geben.
Zu 5.: Jede Rationale Zahl ist eine Reele aber nicht jede Reele rationale - zum Beispiel: Wurzel aus 2 ist keine rationale Zahl aber eine reele
Das verstehe ich nicht. Wenn du weißt, dass die beiden korrekt sind & die anderen nicht, musst du zwangsweise wissen, warum. Ansonsten ist es geraten oder abgeschrieben.
Vielleicht siehst du dir nochmal genau die Zahlenmengen an & welche Zahlenmengen in anderen Zahlenmengen enthalten sind. Dann kannst du alle Fragen beantworten.
Die Lehrerin hat uns die Lösungen mitgegeben. unsere aufgabe ist nur die begründung!!
a) ist falsch.
b) ist richtig.
c) ist falsch (da hast du dich vertan).
d) ist falsch
e) ist falsch
Eine rationale Zahl ist z.B. -5/8
Eine reelle Zahl ist z.B. pi oder 2^0,5
Eine imaginäre Zahl ist z.B. (-3)^0,5. Man schreibt diese Zahl als i3, oder 3i, wobei i = (-1)^0,5 ist, bzw. i² = -1
Eine komplexe Zahl wird normalerweise in der Form a + bi geschrieben, wobei a und b reelle Zahlen sind.
Upps, c) ist ebenfalls eine komplexe Zahl, einfach mit b=0
Wieso soll eine Bruchzahl keine komplexe Zahl sein? Die Zahlenmengen sind ja echte Teilmengen voneinander, d.h. jede Bruchzahl als rationale Zahl ist auch eine reelle Zahl und jede reelle Zahl auch eine komplexe Zahl (eben mit Imaginärteil 0). Außer man setzt bei komplexen Zahlen explizit voraus, dass der Imaginärteil von 0 verschieden sein muss. Aber das ist meines Wissens nach nicht so.
Laut den Lösungen (die wie vom LEHRER bekommen haben) ist es so richtig!
Naja, es kann ja Intuition oder Vermutung sein, ohne es komplett zu raten. Aber solche Sachen wirklich formal zu beweisen ist ja dann nochmal was anderes als "nur" zu entscheiden, ob man der Meinung ist, dass ne Aufgabe richtig oder falsch ist. Vielleicht waren es auch einfach die Lösungen zu so ner Prüfungsaufgabe, wo dann dem Fragesteller nicht klar ist, WARUM die Lösungen so aussehen, weil da dann immer nur die entsprechenden Sachen angekreuzt werden, die aber eben nie erklärt sind.