Kann mir einer bei dieser Mathe Aufgabe helfen?
Ich muss zu dieser Aufgabe eine PL halten und ich verstehe sie nicht

4 Antworten
b ist 3,5 ich
a kannst du easy ermitteln über eine Nullstelle:
0 = a* (5,625 inch)² + 3,5 inch
y = ax^2 + b
Bei dieser Gleichung der Parabel hast du die zwei unbekannten Variablen a und b
Du weißt, dass die beiden Punkte
P1(0, 3.5) und P2(5.625, 0)
Auf der Parabel liegen
Setze diese beiden Punkte in die Parabelgleichung ein, dann ergibt sich
b = 3.5
a = - 0.110617
=>
y = - 0.110617x^2 + 3.5
Vol. = 2 * Integral y^2 * pi * dx von 0 bis 3.5 =
2*integral [0 bis 3.5] π (3.5 - 0.110617 x^2)^2 dx = 207.936 inch^3 =
207.936 * (2.54cm)^3 =
3407.4605 cm^3
Bei 0 anzufangen ist wegen der Symmetrie angebracht. Das Ergebnis kann anschließend mit 2 multipliziert werden. Die 3,5 sind die Nullstelle der y-Achse. Hier liegt offensichtlich ein Versehen vor. Natürlich muß bis 5,625 integriert werden.
Bei 0 anzufangen ist wegen der Symmetrie angebracht.
Das ist klar...
Die 3,5 sind die Nullstelle der y-Achse. Hier liegt offensichtlich ein Versehen vor. Natürlich muß bis 5,625 integriert werden.
Eben, darum gings mir. Deshalb ist auch das Ergebnis falsch.
Vorbemerkung: um das Volumen in cm^3 zu erhalten, rechnen wir alle Maße von inch in cm um.
Scheitelpunkt S: y = 3,5'' = 8,89 cm
Nullstelle N: x = 5,625'' = 14,288 cm
1) Zunächst ermitteln wir die Gleichung der Parabel:
Ansatz: f(x) = ax^2 + b
Punktproben mit S(0/8,89)
8,89 = a * 0^2 + b
b = 8,89
Punktprobe mit N(14,288/0):
0 = a * 14,288^2 + 8,89
a = - 8,89 / 14,288^2 = 0,0435
f(x) = 0,0435 x^2 + 8,89
2) Berechnung des Volumens:
Für das Volumen eine Rotationskörpers um die x-Achse gilt der Ansatz:

mit:
a = - 14,288
b = + 14,288
f(x) = f(x) = 0,0435 x^2 + 8,89
nun integrieren wir:


[...]
= 4213 cm^3 = 4,2 l
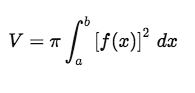
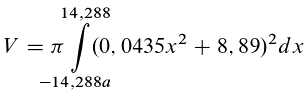
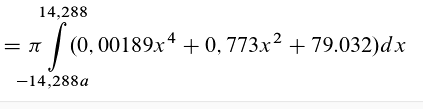
a muß negativ sein, sonst wäre die Parabel nicht nach unten geöffnet.
Korrektes Ergebnis 3783,888771 cm³.
ups.
In dieser Zeile habe ich das Minus verloren:
a = - 8,89 / 14,288^2 = 0,0435
Korrektes Ergebnis 3783,888771 cm³.
Hatte vorsichtshalber zur Kontrolle recherchiert, welches Volumen ein Football tatsächlich hat und da hat chatgpt behauptet, 4,2 l. Deshalb ist mir der Fehler auch nicht aufgefallen.
Passiert leicht. Ich hatte beim ersten Durchrechnen übrigens auch bis 3,5 Inch integriert, aber für die Berechnung von a korrekt mit 5,625 Inch gearbeitet.
Ne kann ich nicht. Ich würde gerne, aber ich kann es wirklich nicht
Warum integrierst du von 0 bis 3,5 und nicht von -5.625 bis +5.625?