Ist 50% und 2 mal 25% das selbe?
Hallo, warum ist 50% wahrscheinlicher als 2 Runden zu spielen mit 25%? Wie berechnet man die Wahrscheinlichkeit für das mit 25%? Es wird, wie ich es mir denken kann nicht 50 ergeben, sondern?
Ich hatte schon zuvor eine ähnliche Frage gestellt nur viel komplizierter in der es leider tendenziell verständlichkeitsprobleme gab, deswegen nun eine simplere Frage, mit der Antwort ich jedoch meine Ursprüngliche Frage beantworten kann.
6 Antworten
Hallo,
wenn Du eine Gewinnwahrscheinlichkeit von 25 % hast, bedeutet das nicht, daß Du bei zwei Spielen zu 50 % und bei vier Spielen zu 100 % gewinnst.
Gewonnen hast Du, wenn Du nicht in allen Spielen verlierst.
Bei zwei Spielen wäre die Chance, ein- oder zweimal zu gewinnen, die Gegenwahrscheinlichkeit zu der Chance, zweimal zu verlieren.
Wenn du zu 25 % gewinnst, verlierst Du zu 75 %.
Die Chance, zweimal zu verlieren ist also (3/4)*(3/4)=9/16.
Ziehst Du das von 1, also von 16/16 ab, bleiben 7/16 übrig. Das ist dann die Chance, daß Du wenigstens einmal gewonnen hast - und sie liegt etwas unter 8/16 oder 50 %.
Herzliche Grüße,
Willy
Was bitte soll hier "offizielle Formel" heißen? Die 1 ist einfach die Wahrscheinlichkeit für alle möglichen Ausgänge zusammen.
Naja wie man die durchschnittswahrscheinlichkeit ausrechnet bei mehreren Runden. Deine Antwort die du unten aufgelistet hast ist zwar gut,
Gewinn Gewinn
Gewinn Verlust
Verlust Gewinn
Verlust Gewinn.
Aber ich brauche eine, ok offiziell vielleicht falsch ausgedrückt aber eine generelle oder allgemeine Formel. Wenn die Chance nicht mehr 25% ist sondern 0,1133 dann kann man nicht mehr so entspannt rechnen und ich habe eine Formel gesucht, die auch für solch komplexe zahlen taugt
Die Wahrscheinlichkeit eines Ereignisses liegt zwischen 0 (trifft auf keinen Fall ein) und 1 (trifft auf jeden Fall ein).
Beim Würfeln mit einem herkömmlichen Würfel wäre 1 die Wahrscheinlichkeit dafür, eine 1; 2; 3; 4; 5 oder 6 zu werfen, denn irgendeine Seite des Würfels wird nach dem Würfeln oben liegen. Die 0 wäre das Werfen einer 7, denn Du kannst keine Augenzahl mit einem einzigen Wurf erzielen, die auf dem Würfel überhaupt nicht vorhanden ist.
Die Wahrscheinlichkeit, beim Würfeln eine bestimmte Zahl zu würfeln - etwa die 3 - liegt bei 1/6, wenn der Würfel nicht gezinkt ist.
Nun darfst Du diese Wahrscheinlichkeit bei mehrmaligem Würfeln nicht addieren, denn sonst hättest Du nach sechsmaligem Würfeln (6*1/6) auf jeden Fall eine 3 dabei und nach siebenmaligem Würfeln stiege die Wahrscheinlichkeit für eine 3 auf 7/6, also auf einen Wert von über 1 und wäre damit sicherer als todsicher.
Wenn Du zweimal würfelst und es auf eine 3 abgesehen hast, gibt es vier Möglichkeiten: Beide Würfe sind eine 3 (1/6*1/6)=1/36.
Der erste Wurf ist eine 3, der andere irgendeine andere Zahl (1/6*5/6=5/36), denn die Wahrscheinlichkeit für eine andere Zahl als 3 ist 5/6.
Es kann auch der erste Wurf eine andere Zahl sein und erst der zweite eine 3. Dann ergibt das eine Wahrscheinlichkeit von 5/6*1/6=5/36.
Oder Du hast Pech und wirfst gar keine 3, das wäre dann 5/6*5/6=25/36.
Das sind alle Möglichkeiten die eintreffen können und sie ergeben zusammen
1/36+5/36+5/36+25/36=36/36=1. Da sich all diese vier Ereignisse gegenseitig ausschließen und alle Möglichkeiten abdecken, ergänzen sie sich zu 1.
Das einzige Ereignis, bei dem keine 3 geworfen wird, hat eine Wahrscheinlichkeit von 25/36. Die restlichen 11/36 bis zur 1 sind somit die Wahrscheinlichkeit dafür, daß wenigstens einmal eine 3 erscheint, nämlich beim ersten Wurf, beim zweiten oder bei allen beiden.
Wenn Du auf diese Art rechnest, erkennst Du, daß die Wahrscheinlichkeit für das Werfen einer 3 niemals die 1 erreicht - egal, wie oft du würfelst - weil es immer die Möglichkeit gibt, daß bei keinem Deiner Würfe eine 3 erscheint.
Ah und kleine Ergänzung, nicht P sondern dass Gegenereignis also 1-P, so ist die Rechnung korrekt und müsste für alle und beliebiglange Wahrscheinlichkeiten gelten, richtig? 1-(1-P*1-P*...) und um auszurechnen nach wie vielen Runden man eines der Ergebnisse im Schnitt bekommt 100/(1-(1-P*1-P*...))
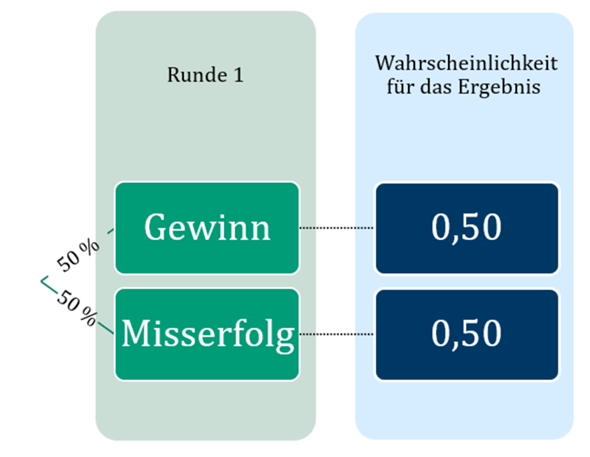
Bei einer Runde mit 50 % Gewinnwahrscheinlichkeit beträgt die Wahrscheinlichkeit für einen Gewinn...

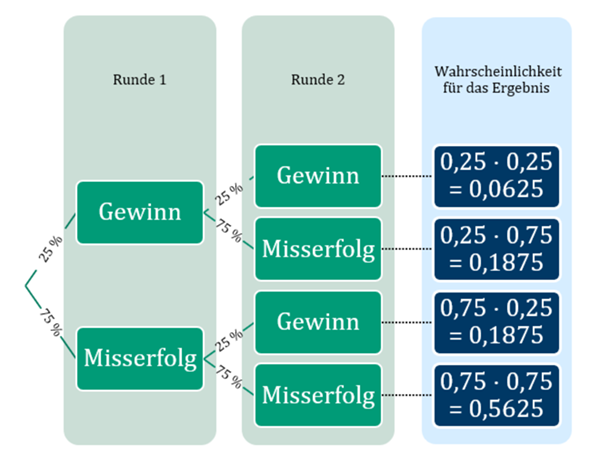
Bei 2 Runden, jeweils mit Gewinnwahrscheinlichkeit 25 %, beträgt die Wahrscheinlichkeit für mindestens einen Gewinn...

============
Der Erwartungswert für die Anzahl der Gewinne ist aber in beiden Fällen gleich groß.
Im 1. Fall:
0,50 ⋅ 1 + 0,50 ⋅ 0 = 0,50
Im 2. Fall:
0,0625 ⋅ 2 + 0,1875 ⋅ 1 + 0,1875 ⋅ 1 + 0,5625 ⋅ 0 = 0,50
bzw. (0,25 ⋅ 1 + 0,75 ⋅ 0) + (0,25 ⋅ 1 + 0,75 ⋅ 0) = 0,25 + 0,25 = 0,50
Der Erwartungswert ist gleich groß, obwohl im 2. Fall die Wahrscheinlichkeit für mindestens einen Gewinn kleiner ist. Das liegt daran, dass man im 2. Fall auch mit 6,25 % die Möglichkeit hat 2-mal hintereinander zu gewinnen. Dieser mögliche Doppelgewinn gleich beim Erwartungswert die kleinere Wahrscheinlichkeit für mindestens einen Gewinn aus.
Willy1729 hat das schon korrekt beantwortet, ich will das noch mal ergänzen.
Wenn du zwei Runden spielst, dann gibt das vier Möglichkeiten, wie das ausgehen kann:
Gewinn Gewinn
Gewinn Verlust
Verlust Gewinn
Verlust Gewinn.
Die Wahrscheinlichkeit, dass du zweimal gewinnst, ist 1/4 * 1/4 = 1/16
Die Wahrscheinlichkeit, dass du beim ersten Mal gewinnst und beim zweiten Mal verlierst, ist 1/4 * 3/4 = 3/16.
Die Wahrscheinlichkeit, dass du beim ersten Mal verlierst und beim zweiten Mal gewinnst, ist 3/4 * 1/4 = 3/16.
Die Wahrscheinlichkeit, dass du zweimal verlierst, ist 3/4 * 3/4 = 9/16.
Dich interessieren alle Fälle, in denen du mindestens 1x gewinnst, ja?
Das sind die ersten drei Fälle. Wenn du die drei Wahrscheinlichkeiten addierst, dann kommst du auf
1/16 + 3/16 + 3/16 = 7/16.
Das ist gerade etwas weniger als 0,5.
(Du kannst es auch - wie Willy - mit dem Gegenereignis berechnen).
Deinen Denkfehler hatte ich auch mal.
Man kann eine Wahrscheinlichkeit über mehre Runden hinweg nicht mit der Wahrscheinlichkeit einer Runde vergleichen. Deine Gewinnchance pro Runde ist und bleibt 50%!
Deswegen Rede ich ja von 2 Runden. Zwei Runden mit 25% Chance und nur einmal muss man gewinnen. Durchschnittswahrscheinlichkeit zwischen 25-50% Aber was genau...
Extrembeispiele verdeutlichen meistens sehr gut wieso dein Gedankengang nicht aufgeht.
Ist es besser 1x100% Gewinnchance zu haben oder 100x1%?
Natürlich kann man jetzt sagen - aber Moment mal. Wenn ich 100 mal spiele, dann gibt es die Chance mehrmals zu gewinnen. Es gibt aber halt auch die Chance gar nicht zu gewinnen. Deswegen nennt man es ja auch "Wahrscheinlichkeit" und nicht "praktische Berechnungen".
Wenn deine Gewinnchance 1% beträgt, dann sind diese 1% jede Runde aufs neue 1%. Deine Gewinnchance insgesamt ist natürlich höher, da du mehr Runden spielst. Das ist den 1% in der aktuellen Runde aber vollkommen egal. Deswegen kann man die zwei Zahlen (auch wenn es beides Prozentzahlen sind) nicht miteinander vergleichen.
Spielst Du zweimal mit 25% Gewinnwahrscheinlichkeit, verlierst Du jeweils mit 75% Wahrscheinlichkeit.
Zu 56,25% verlierst Du zweimal. Zu 6,25% gewinnst Du zweimal. Und zu 37,5% gewinnst Du einmal.
Ah, also ist die Offizielle Formel 1-(P*P*...) also in dem Beispiel 1-(3/4*3/4) also müsste man im Schnitt einen Erfolg von 43,75% haben. Klingt realitisch. Wie die 1 Zustande kommt hinterfrage ich jetzt mal nicht... Aber vielen Dank. Das war gesucht