Hilfe Aufgabe Mathe?
Hallo , lerne gerade für eine klassenarbeit und steht komplett auf dem Schlauch... wichtig: das ist keine Hausaufgaben Aufgabe sondern eine Aufgabe die ich mir selber zum lernen raus gesucht habe. "Ein Haus ist 12,4 m breit, Die Höhe des giebels beträgt 4,10m. Berechne die Länge der dachsparren wenn diese 80 cm überstehen " wichtig vllt dazu zu sagen : sind gerade beim Thema satzgruppe des Pythagoras. Danke für eure Hilfe .
8 Antworten
Hallo hna1234.
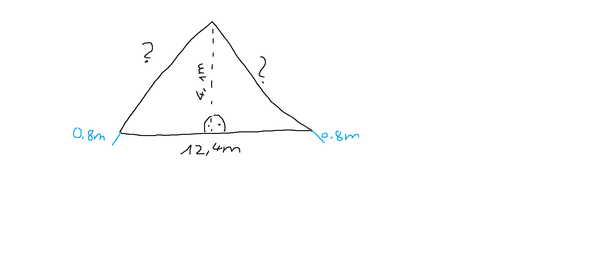
Ich habe dir mal eine einfache Skizze mit Paint gezeichnet, die du im Bild siehst :)
Die Seiten, wo die Fragezeichen stehen, sollst du berechnen.
Die gestrichelte Linie ist die Höhe des Giebels. Damit kannst du dir dann zwei gleich große, rechtwinklige Dreiecke konstruieren. Damit kannst du dann auch wieder den Satz des Pythagoras nutzen.
Wir nehmen also einfach mal das linke Dreieck und wollen nun die Länge der linken Seite berechnen. Die linke Seite mit dem Fragezeichen ist die Hypotenuse, also die Seite c. Die anderen beiden Seiten sind die Katheten. Die eine ist die Höhe des Giebels und somit 4,1m lang. Die andere ist genau halb so lang die das Haus breit ist, also 12,4 : 2 und somit 6,2m.
Also nochmal zusammengefasst:
a = 4,1m
b = 6,2m
c = ?
Der Satz des Pythagoras lautet:
a² + b² = c²
Nun setzten wir ein:
4,1² + 6,2² = c²
Nun auflösen, sodass links nur noch eine Zahl steht.
16,81 + 38,44 = c²
55,25 = c² |√
c ≈ 7,43m
Nun müssen wir noch die 80cm (0,8m) dazu rechnen, die überstehen.
7,43m + 0,8m = 8,23m
Damit sind die Dachsparren ca. 8,23m lang!
______________________________________________________
Falls du noch Fragen hast, melde dich einfach ;)
Liebe Grüße
TechnikSpezi
1. Schritt : den Giebel zeichnen,du siehst dann ein Dreick und wenn du die Höhe h=4,10 m einzechnest,dann ergeben sich 2 "rechtwinklige Dreiecke"
Satz des Pythagoras c^2=a^2+b^2 siehe mathe-Formelbuch Kapitel "Geometrie"
hier ist c=s und a=12,4m/2=6,20 m und b=h=4,10 m
S^2=a^2+b^2 ergibt S=Wurzel(6,2^2+4,1^2)=7,433 m
nun noch die 80 cm=0,80 m hinzuaddieren
Gesamtlänge also Sges=7,433 m+0,8 m=8,233 m
Mach Dir auf jeden Fall eine Skizze der relevanten Angaben!
Unten deutest Du ein Rechteck an (das Haus), darauf ist ein Dreieck, dessen Spitze genau in der Mitte ist (so sind die meisten Dächer gebaut; ansonsten wäre die Aufgabe auch nicht lösbar).
Breite des Hauses und Höhe des Daches kennst Du. Dann sollte Dir der Satz des Pythagoras ins Auge springen.
Wichtig: die Dachsparren stehen 80 cm über (damit Du darunter trocken stehen kannst!), d.h. die musst Du nachher zu Deinem Ergebnis dazurechnen.
Zum Vergleich mein Ergebnis: 8,233 m.
Der Giebel ist 4,10m hoch, das ist die eine Kathete.
Das Haus ist 12,4m breit, die Hälfte davon ist
die andere Kathete. Die Dachsparren sind die
Hypothenuse, sie sind
0,8 + √(4,1² + 6,2²) = 8.23m
lang. Die 0.8 kommt von dem Überstand.
Eine Skizze sollte helfen, kann es mir selbst ohne nur schwer vorstellen, wo genau da jetzt ein Dreieck bzw. der Satz des Pythagoras helfen könnte :)
Vielleicht sowas wie (12,4+0,8)^2+4,10^2=c^2
vielen lieben dank:) sehr gut erklärt:)