Satz des Pythagoras: Dreidimensionale Figuren
Wir lernen in der Schule gerade die Satzgruppe des Pythagoras kennen und haben eine Ha zum Knobeln aufbekommen. Meine Frage: Wie errechnet man die Hypothenuse bei dreidimensionalen Figuren? Danke schonmal im Voraus :)
6 Antworten
Es soll sozusagen ein Saftpäckchen sein, dass die Höhe 7,2 cm, Breite 6,3 cm und die Tiefe 3,2 cm hat.
Und was ist gesucht?
Wahrscheinlich die Länge eines Strohhalms, der an einer Ecke eingesteckt wird und nicht ganz verschwinden soll oder etwas Ähnliches.
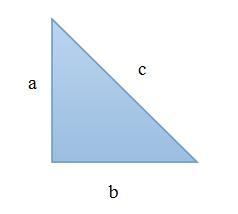
Hypotenusen gibt's nur in rechtwinkligen Dreiecken, und das sind nun mal zweidimensionale und nicht dreidimensionale Figuren.
Was du z. B. im Dreidimensionalen ausrechnen kannst, ist die Länge der Raumdiagonalen eines Würfels mit bekannter Seitenlänge (mit zweimaliger Anwendung des Satzes des Pythagoras).
Vermutlich hat die dreidimensionale Figur dreieckige Seitenflächen. Mit diesen kannst du dann arbeiten.
Über Flächen kannst du dir Seiten Länge ausrechnen, das selbe auch über das Volumen. Groß helfen kann man dir gerade nicht, da wir keine Angaben haben.
a2 + b2 = c2
(a*a+b*b=c*c)
Mit h = 7,2 und b = 6,3 und t = 3,2 rechnest Du zuerst die Diagonale
d der Grundfläche aus: d² = b² + t². Dann die Raumdiagonale D von
einer Ecke zur entferntesten anderen Ecke D² = d² + h² = b² + t² + h²