Hebt sich Zeitdilatation mit der gravitativen Zeitdilatation auf?
In der Relativitätstheorie gibt es ja die Zeitdilatation. Bei der normalen Zeitdilatation vergeht die Zeit langsamer bei relativ zum Betrachter bewegten Systemen. Bei der Gravitativen Zeitdilatation vergeht die Zeit schneller je schwächer die Gravitation ist. Wie wäre es dann wenn man sich relativ schnell in einem relativ schwachen Gravitationsfeld bewegt. Könnten sich die Zeitdilatationen dann aufheben?
6 Antworten
Du hast hier eine Überlagerung zweier Effekte. Du musst beide in die Rechnung einbeziehen. Manchmal überwiegt die Zeitdilatation durch die Geschwindigkeit, manchmal die durch die Gravitation. Als Faustregel gilt: Die natürliche Bahn, also der freie Fall jedes Körpers ist diejenige Kurve, auf der eine Uhr am schnellsten läuft.
Beispiel 1: Wenn du eine Uhr hoch wirfst und wieder fängst, während eine andere Uhr in deiner Hand ruht, ist der Zeiger der hoch geworfenen Uhr weiter gegangen. Denn die Uhr in deiner Hand ist nicht im freien Fall.
Beispiel 2: Alle Uhren auf Meereshöhe laufen gleich schnell. Dazu wäre eine komplizierte Rechnung nötig, weil der Meeresspiegel am Äquator durch die Erdrotation höher ist, aber auch schneller bewegt wird. Mit der obigen Faustregel siehst du aber sehr schnell und ohne Rechnung, dass die Uhren gleich schnell laufen. Denn würde die Zeit nicht für alle Wassermoleküle auf dem Meeresspiegel gleich schnell laufen würde, so würden sich diese Wassermoleküle so lange verschieben, bis dies wieder ausgeglichen wäre.
Beide Effekte müssen berücksichtigt werden, damit das GPS funktioniert. Es handelt sich hier also nicht nur um eine Theorie, sondern um Physik, die im Alltag immer wieder bestätigt wird.
Richtig. Aber du hast in diesem Beispiel eben die zwei Effekte, die sich überlagern. 1. Die Uhr die hoch geworfen wird, hat eine Anfangs- und eine Endgeschwindigkeit und geht deshalb langsamer. 2. Weil sie aber immer höher oben ist als die ruhende Uhr, geht sie schneller.
Eigentlich ist das eine ziemlich mühsame Rechnung, beide Effekte auszurechnen und zu schauen, welcher grösser ist. Aber mit der Faustregel siehst du sofort: Der zweite Effekt ist der grössere. Denn die hoch geworfene Uhr macht den Weg ohne Krafteinwirkung, während die untere ständig durch elektrische Kräfte vom Boden 'beschleunigt' wird. Die Kraft, die zum Hochwerfen aufgewendet wird, geht dagegen nicht in die Rechnung ein. Denn diese ist nicht dauerhaft. Gerade kurz nach dem Abwurf gehen die Uhren noch synchron. Die Verschiebung passiert erst während des Flugs.
Allerdings ist die Faustregel während der Zeit der Abschuss-Beschleunigung tatsächlich unklar. Denn es gibt verschiedene Arten, wie ein Körper beschleunigt werden kann: Werden alle Teile der Uhr gleichzeitig, nämlich vom Ruhesystem aus gleichzeitig beschleunigt, dann wird er so beschleunigt, dass es keine Längenkontraktion gibt? - Dann würde die Uhr bei starker Beschleunigung auseinander gerissen. Wenn die Uhr nicht auseinander gerissen werden soll, musst du definieren, welcher Punkt der Uhr gleichmässig beschleunigt wird.
Ein gutes Buch, um solche Überlegungen zu üben ist Jürgen Brandes, 'Die relativistischen Paradoxien und Thesen zu Raum und Zeit'.
Dein Energiebedarf steigt je schneller du wirst. Energie ist äquivalent zur Masse. Dein Gravitationsfeld wird also eher größer.
Du müsstest jetzt ein Gerät entwickeln, dass deine Masse wieder verkleinert. Wenn dieses aber wieder Energie benötigt, wäre das Kontraproduktiv. Ein Gerät was Energie entzieht würde dich wiederum verlangsamen.
Das einzige was dem entsprechen könnte, wäre vermutlich ein Wurmloch - eine Abkürzung durchs Weltall. Du würdest zwar super schnell von A nach B kommen ohne aber den hohen Energieaufwand und müsstest somit mit wenig Zeitdifferenz hin und zurück springen können.
So zumindest meine Vermutung. Kommt auch darauf an wie das Wurmloch aufgebaut ist (ist es ein riesiger Energiestrang oder Dimensionsknoten oder oder).
Ohne die sind wir verloren — oder sie gingen ohne uns verloren.
Ja, die englische Wikipedia hat sogar eine Grafik dazu, in welcher Höhe sich bei einem Erdorbit die beiden Effekte aufheben: https://en.wikipedia.org/wiki/Time_dilation#/media/File:Time_Dilation_vs_Orbital_Height.png
Hallo MartinNavi,
ja, es gibt Kombinationen aus Höhe und Geschwindigkeit, für die eine Uhr an Bord eines Luftfahrzeug mit einer Uhr auf der Erde gerade synchron bzw. isochron läuft.
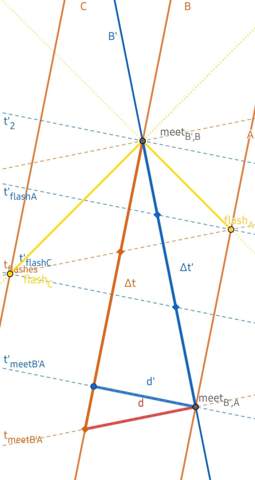
Mir gefällt allerdings das Wort „Zeitdilatation“ nicht, weil es irreführend ist, insbesondere wenn es um zwei mit konstanter Geschwindigkeit (nicht nur Tempo!) relativ zueinander bewegte Raumfahrzeuge B und B' geht. Schließlich kann man insbesondere dann jeden der beiden als ruhend und damit den Zeittakt seiner Uhr als verlängert interpretieren.
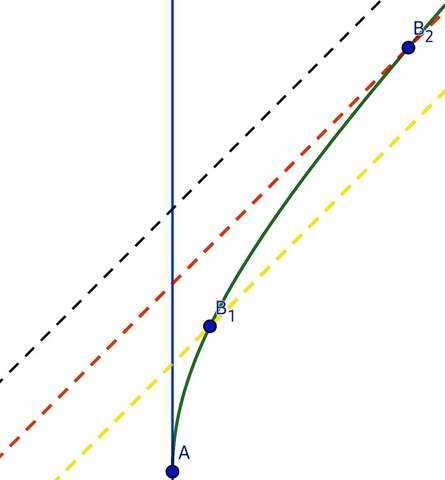
Betrachtet man das Ganze in einem Raumzeit- Diagramm, sieht man, dass die unterschiedlich langen Zeiten ganz andere Strecken in der Raumzeit darstellen, nämlich ein mal einen Vorgang an Bord von B' und ein mal dessen Projektion auf die Weltlinie (WL) von B, die Koordinatenzeit Δt, in der B' die räumliche Strecke
(1) Δs = √{Δx² + Δy² + Δz²}
zurücklegt. Die eigentliche Dauer eines Vorgangs, die Eigenzeit
(2) Δτ = √{Δt² − Δs²⁄c²},
gleichsam die Länge der raumzeitlichen Strecke zwischen Anfang und Ende des Vorgangs bleibt gleich.
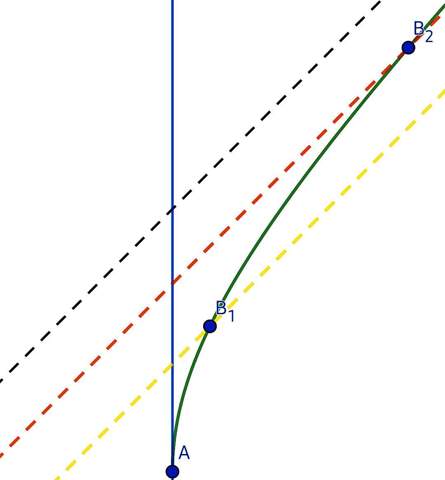
Die Idee, Gravitation als Krümmung der Raumzeit zu interpretieren, beruht auf der Tatsache, dass die auf einen Körper wirkende Kraft proportional zu dessen Masse ist - genau wie eine Trägheitskraft. Wenn man ein Raumfahrzeug gleichförmig beschleunigt, kann man sich vorstellen, der Einzige zu sein, der sich einem homogenen Gravitationsfeld widersetzt, in dem andere Körper frei fallen. Hinter dem Fahrzeug entsteht dadurch ein Ereignishorizont (EH), eine Raumzeit-Fläche, von der der Reisende nichts erfährt, solange er die Beschleunigung fortsetzt.
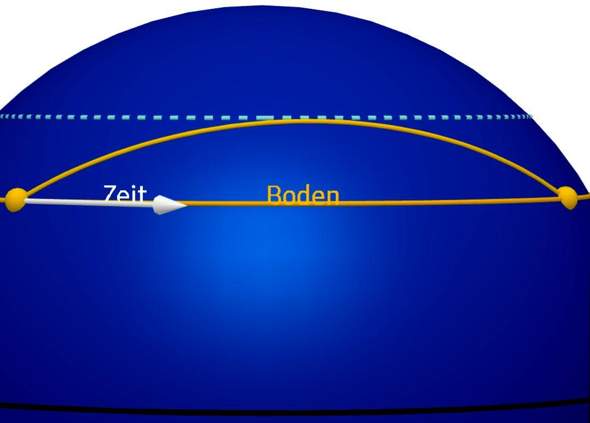
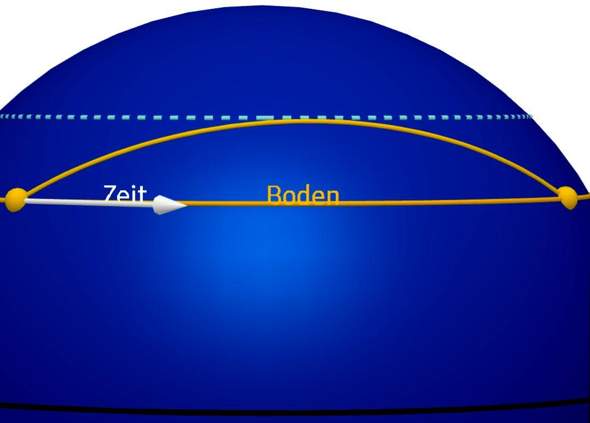
Ein Raumfahrzeug, in dem keine Trägheitskräfte auftreten, hat eine geodätische WL, also eine, die so gerade wie möglich ist. Auf einer Kugeloberfläche etwa sind die geodätischen Linien Großkreise.
Einen Großkreis- Bogen beschreibt auch ein Flugzeug, das den kürzesten Weg zwischen zwei Orten nimmt, die etwa auf demselben Breitengrad liegen, der seinerseits ein Kleinkreis ist. Dies ist ein Modell für einen senkrechten Sprung nach oben.
Weglängen sind im Allgemeinen Integrale, d.h., sie setzen sich aus sehr vielen sehr kleinen Strecken zusammen. In Polarkoordinaten ist die Eigenzeit
(3) dτ = √{dt² − (dr² + r²dΩ²)⁄c²},
wobei dΩ eine Abkürzung für den tangentialen Teil dθ + sin(θ)dφ ist. Die radiale Koordinate r steht für eine Kugelschale dee Fläche 4πr² um den Ursprung und ist hier zugleich noch der Abstand
Sitzt im Ursprung bzw. um ihn herum eine kugelsymmetrische Masse M, so hat diese den Gravitationsradius 𝑚 = G∙M⁄c² mit der Gravitationskonstanten G ≈ ⅔×10⁻¹⁰m³⁄(s²kg), was bei einer Erdmasse knapp 4⁄9cm ausmacht.
Das Gravitationsfeld deformiert (3) außerhalb der Massenverteilung zur SCHWARZSCHILD- Metrik
(4) dτ = √{dt²(1 − 2𝑚⁄r) − (dr²⁄(1 − 2𝑚⁄r) + dΩ²)}.
Damit ist der Abstand zwischen benachbarten Kugelschalen größer als r, und falls die Massenverteilung innerhalb der Kugelschale mit dem SCHWARZSCHILD-Radius 2𝑚 liegt, ist der Bereich r < 2𝑚 ein Schwarzes Loch (SL). Dort ist r zeitartig (mit Richtung nach innen), sodass jemand, der dort hingerät (was von außen betrachtet unendlich lange dauert), sich gleichsam in einem kollabierenden Raum wiederfindet und durch Gezeitenkräfte auseinandergerissen wird.
Bei r = 2𝑚 selbst liegt der (absolute) EH des SL, falls es nicht rotiert oder elektrisch geladen ist. Die SCHWARZSCHILD-Koordinaten sind nicht sehr gut geeignet, ihn zu beschreiben, weil (4) dort singulär wird. Das lässt sich aber beheben.
Die SCHWARZSCHILD- Metrik ist für den Außenraum allerdings auch in der Nähe der Erde oder im Sonnensystem eine gute Näherung für die realen Verhältnisse und bieten somit eine gute Möglichkeit, auszurechnen, welche Höhe zu welchem Tempo gehört.
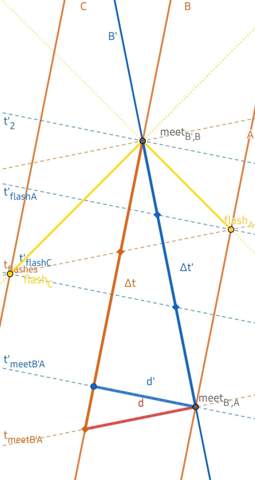
Nein. Die Zeit wird nicht schneller in einem schwachen Gravitationsfeld, sondern nur langsamer in einem starken Gravitationsfeld.
Du berücksichtigst nicht, dass eine Uhr auf der Erdoberfläche nicht eine weit entfernte inertiale Uhr ist, sondern in einem Gravitationstrichter steckt.
Erstmal danke für die Antwort. Bezüglich des 1. Bsp...dachte ich aber das laut der Relativitätstheorie schnell bewegte Uhren langsamer vergehen. Und wenn du sie hoch wirst wird sie ja beim Fall beschleuningt.