Ganzrationale Funktion dritten Grades?
Moin, ich brauche Hilfe bei Mathe...
Bestimmen Sie eine ganzrationale Funktion dritten Grades: Der Graph verläuft durch den Ursprung mit der Steigung -1 und schneidet die x-Achse im Punkt P(1|0) mit der Steigung 2.
Also die allgemeine Darstellung der Funktion dritten Grades ist ja f(x)=ax³+bx²+cx+d
Wie bestimme ich daraus jetzt die Funktion mit den geforderten Eigenschaften?
Danke schon mal im vorraus :)
5 Antworten
4 Unbekannte, 4 Bedingungen: lösbar. Dazu müssen wir 4 Gleichungen aufstellen.
f(x) = ax³+bx²+cx+d
f'(x) = 3ax^2 + 2bx + c
P(0/0):
0 =0+0+0+d
also:
d = 0
P(1/0):
0 = a + b + c
f'(0) = -1:
-1 = c
f'(1) = 2:
2 = 3a + 2b -1
3a + 2b = 3
aus 0 = a + b + c folgt mit c = -1:
a + b = 1
Wir haben also 2 Gleichungen übrig:
3a + 2b = 3 (1)
a + b = 1 (2)
aus 2 folgt:
b = 1 - a
eingesetzt in 1:
3a + (1 -a) = 3
nach a auflösen:
3a + 1 - a = 3
2a = 2
a = 1
in b = 1 - a eingesetzt:
b = 1 - a = 1 - 1 = 0
Damit lautet f(x):
f(x) = 1x^3 + 0x^2 + (-1)x + 0
f(x) = x^3 - x
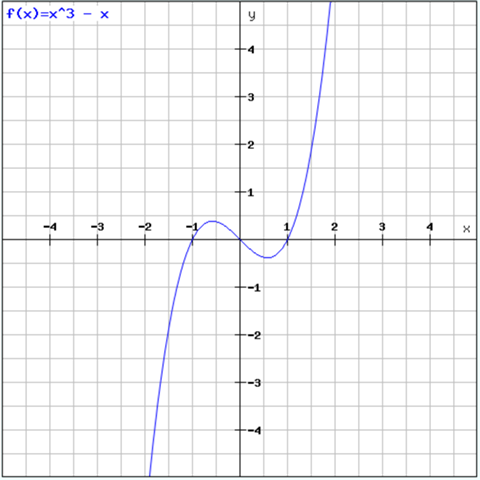
Und so sieht der Graph aus:
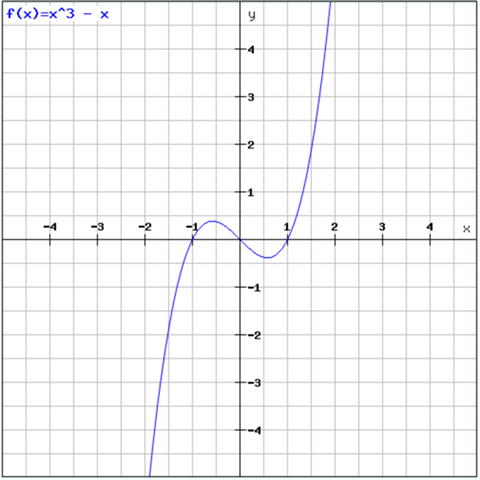
..und siehe da, die Punkte stimmen und die Steigung in den Punkten auch.
aber als hilfreichste antwort auszuzeichnen ist dir zu viel Mühe ?
Ich glaube, manche user wissen gar nicht, dass es diese Funktion gibt.
Du kannst aus den Daten entnehmen, dass
f(0)=0
f'(0)=-1
f(1)=0
f'(1)=2
Das setzt du dann ein
( bei f' 3ax²+2bx+c )
0= d
-1= c
0= 1a+1b+1c+d
2= 3a+2b+c
Da du c und d schon hast, kannst du die weglassen. Also setzt du die beiden anderen Gleichungen ineinander ein.
0 = 1a+1b I × 2
2 = 3a+2b
_____
0 = 2a+2b
2 = 3a+2b
Dann subtrahieren
2 = a
Und b ist gleich 0 = 2 + 1b also b = -2
Die Formel ist dann
f(x)= 2x³-2x²-1x
Wie bestimme ich daraus jetzt die Funktion mit den geforderten Eigenschaften?
Du schaust Dir an, was für Informationen gegeben sind, und was sie Dir bringen:
Der Graph verläuft durch den Ursprung
f(0) = 0
mit der Steigung -1 und
f'(0) = -1
schneidet die x-Achse im Punkt P(1|0)
f(1) = 0
mit der Steigung 2.
f'(1) = 2
4 Informationen, 4 Gleichungen, 4 Unbekannte. Passt.
Gleichungssystem aufstellen und mit einem Lösungsverfahren Deiner Wahl lösen.
f(0)=0
f‘(0)=1
f‘(1)=2
f(1)=0
Nach der ersten Antwort habe ich den Rest schon selber hinbekommen,aber trotzdem vielen Dank. Das bestätigt noch mal,dass ich alles richtig gemacht habe :)