Funktion?
Kann mir jemand bitte bei der Aufgabe 2,3,4 und 6 helfen darf kein Logarithmus ziehen

2 Antworten
Aufgabe 2:
Achsenschnttpunkt:
y-Achse: f(0) = 4 - e^0 = 4 - 1 = 3
x-Achse:
0 = 4 - e^(0,5x)
e^0,5x = 4
ln e^0,5x = ln 4
0,5x = ln4
x = 2ln4 = 2,77
Asymptoten:
x -> +∞ :
e^(0,5x) -> ∞
- e^(0,5x) -> -∞
f(x) -> -∞
x -> - ∞ :
e^(0,5x) -> 0
- e^(0,5x) -> 0
f(x) -> 4
Asymptote für x -> - ∞ bei y = 4
Wertetabelle:

Zeichnung:

Aufgabe 6c:
Ansatz:
f(x) = -0,5 e^(2x) + c
f(1) = 0
-0,5 e^(2*1) + c = 0
c = 0,5e^2 = 3,69
Lösung:
f(x) = -0,5 e^(2x) + 0,5e^2

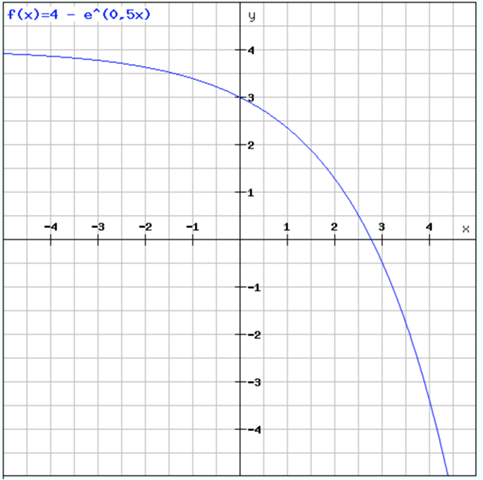
Aufgabe 2:
y-Achsenschnittpunkt: f(0)
x-AS x=0 und ohne ln-Ziehen nur e^1/2x=4
Asymptote: wenn x -> unendlich, dann e^(..) gegen unendlich, also f(x) -> -unendlich
wenn x-> -unendlich, dann e ->0, also f(x) =4
horizontale Asymptote bei y=4
3.
Einsetzen dann bis du ohne ln kommst, so weit wie es geht vereinfachen
4.
Die Funktion fällt, also ist k negativ.
Für große x nähert sich der Graph der y-Wert von b an, also b ≈ 1.
Bei x = 0 ist y ≈ 3, daher ist a + b ≈ 3 → a ≈ 2.
6.
negativ ex. wachsend
verschoben um +3 nach oben (y-Richtung)
Asymptote bei y=3
C wird in y-Richtung verschoben, sodass sie die x-Achse bei x = 1 schneidet.
→ Wir wollen: Ansatz f(1) = 0
Kannst dann selbst auf die weitere Idee kommen