Fläche zwischen zwei Kurven berechnen über und unter der x-Achse?
Hallo Leute!
Ich soll die Fläche zwischen den Schnittpunkten der Funktionen f(x)=2x und g(x)=x²-1 berechnen. Die x-Werte der Schnittpunkte sind 1-wurzel(2) und 1+wurzel(2).
Um die Fläche zu berechnen habe ich das Integral von f(x) und g(x) gebildet und subtrahiert und dann eben die Schnittpunkte eingesetzt. Ich komme auch auf das richtige Ergebnis (8wurzel(2))/3.
Ich versteh nur nicht, warum das richtig ist, da ja ein Teil der Fläche unter der x-Achse und der andere darüber liegt. Wenn ich z.B. die Fläche einer Sinus-Kurve ausrechne, muss ich ja auch die Fläche über und unter der x-Achse berechnen? Warum ist das in diesem Fall möglich und gibt es vielleicht Ausnahmen, bei denen man das nicht so berechnen kann?
Danke!
1 Antwort
Das ist deshalb richtig, weil es nur auf die Differenzfunktion ankommt :
d(x) = f(x) - g(x)
d(x) = 1 + 2 * x - x ^ 2
Und wenn du dir diese Funktion zeichnen lässt :
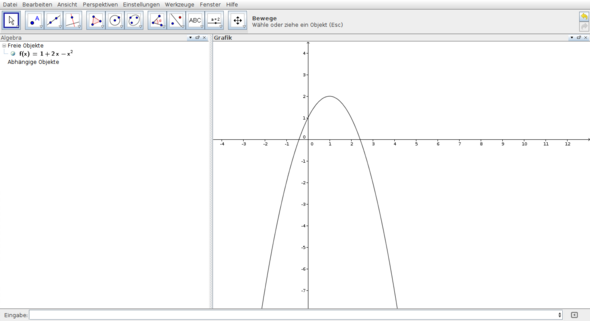
(auf das Bild klicken, um es zu vergrößern !)
Dann kannst du sehen, dass die Differenzfunktion in dem betroffenen Intervall die ganze Zeit oberhalb der x-Achse verläuft, und es keinen Bereich innerhalb des Intervalls gibt, indem sie anfängt unterhalb der x-Achse zu wandern.
Deshalb kann die Differenzfunktion ohne Probleme integriert werden, ohne dass man Flächen mit unterschiedlichen Vorzeichen hat, welche sich gegenseitig "auslöschen" würden.
Das spielt keine Rolle. Begründung: Mann kann zu beiden Funktionsgleichungen die gleiche Konstante addieren, so dass beide über der x-Achse liegen. Am Integral ändert sich nichts, da diese Änderung sich in der Differenz der Stammfunktionen heraushebt...
Aufpassen muss man nur, wenn sich die Funktionsgraphen mehr als einmal schneiden...
Ziehst Du die kleinere Funktion von der größeren ab, dann wird die Fläche, die die Differenzfunktion mit der x-Achse einschließt unterhalb der x-Achse liegen, d. h. beim berechnen der Fläche wird ein negativer Wert rauskommen. Davon nimmt man dann einfach den Betrag.
Würdest Du hier z. B. g(x)-f(x) rechnen, käme als Differenzfunktion x²-2x-1 raus, d. h. der Graph aus "precursors" Bild, nur eben an der x-Achse gespiegelt, also nach oben offen...
... ohjeh, ich sehe gerade: Frau kann das natürlich auch...
...un es muss heißen: mehr als zweimal...
Eine Frage hätte ich noch: Welche Funktion muss ich subtrahieren. Ich habe wo gelesen "obere minus untere Funktion" ist das richtig?
Wenn Du als Ergebnis eine positive Fläche haben möchtest, ist das richtig.
Da aber ohnehin nur der Betrag der Fläche interessiert, ist es letztlich wurscht, welche Funktion Du von welcher abziehst.
Ok, danke für die Antwort. Kann es auch sein, dass die Differenzfunktion in dem gesuchten Intervall unterhalb bzw. unter und über der x-Achse liegt? (nicht für dieses Beispiel)