Ein Erdwall hat im Querschnitt näherungsweise die Form einer Parabel. Er ist 2 m hoch und auf 1 m Höhe 10 m breit. Wie breit ist er am Boden?

Kann mir jemand bitte helfen

Answer 1

[verreisterNutzer]

Aus dem Kommentar zur Antwort von DerRoll

ich soll es in die PQ Formel einsetzen und genau das verstehe ich nicht

... was das mit der pq-Formel zu tun haben sollte, verstehe ich jetzt auch nicht, da man die pq-Formel für die Nullenstellenberechnung der Funktion überhaupt nicht benötigt, wenn man der Antwort von DerRoll folgt.

$f\left(x\right)=a\cdot x^2+2\$ $f\left(5\right)=1\ \to a\cdot5^2+2=1\ \to a=-\frac{1}{25}$

Damit:

$f\left(x\right)=-\frac{1}{25}x^2+2$

Jetzt rechnest Du die Nullstelle aus und bekommst direkt

$x_{1/2}=\pm\sqrt{50}$

Und damit ist die Breite am Boden
$b\ =\ \sqrt{50}-\left(-\sqrt{50}\right)=2\sqrt{50}=2\sqrt{2\cdot5^2}=10\sqrt{2}$

Skizze:

Answer 2

[Wechselfreund]

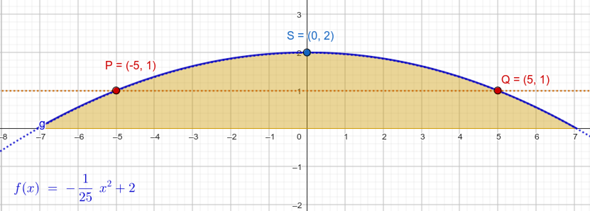
Viele Wege führen nach Rom, hier meine Version:

x-Achse in 1m Höhe

f(x) = a(x-5)(x+5)

f(0) = 1= a (-25) (2m -1 m = 1m)

a = -1/25

Gesucht jetzt f(x) = -1

-1 = -1/25(x-5)(x+5) |* (-25)

25 = x²-25

50 = x²

Answer 3

[Thommy8214]

Das ist eine typische sogenannte Steckbriefaufgabe. Du solltest aus den Angaben erst mal die Funktion finden.

f(x) = a*x^2 + b*x + c ist der Ansatz und du musst die Variablen a, b und c finden.

f(0) = 2

f(5) = 1

f,(-5) = 1

Gleichungssystem erstellen und lösen und dann f(x) = 0 setzen um die Dammbreite zu ermitteln.

Weitere Infos siehe bei DerRoll und evtldocha.

Woher ich das weiß: Studium / Ausbildung

Answer 4

[DerRoll]

Wähle das Koordinatensystem so dass der Scheitelpunkt der Parabel genau auf der y-Achse liegt. Welche Formel hat die Parabel dann? Welche Werte sind noch nicht bekannt? Bei welchem y-Wert liegt der SCheitelpunkt? Welchen Funktionswert hat die Parabel bei x = 5? Warum? Setze nun ein und löse geeignet nach dem noch fehlenden Wert auf.

Comments

[Leasforlive]

ich soll es in die PQ Formel einsetzen und genau das verstehe ich nicht

[DerRoll]

@Leasforlive

Hast du denn schon die ersten beiden Schritte die ich aufgeschrieben habe durch geführt? Wie genau sieht deine Funktion denn nun aus und was ist der unbekannte Wert?