Berechnung gleichmäßig verzögerte Bewegung?
Die Aufgabenstellung ist
Ein Auto steigert bei einer Strecke s=125m seine Geschwindigkeit von V1= 15m/s auf V2= 28m/s
Wie groß sind die zum entlangangfahren der Strecke s erforderliche Zeit t und die Beschleunigung a?
Ich schreibe morgen eine Klausur und würde gerne einen Lösungsansatz bekommen, da ich leider nicht weiß wie ich das lösen soll. Hab schon a=∆V/∆t versucht, aber da fehlen mir ja zwei unbekannte
5 Antworten
Hallo Ilite,
Deine Überschrift
Berechnung gleichmäßig verzögerte Bewegung?
ist irreführend. Schließlich wird der Wagen ja schneller. Das ist aber nicht so relevant.
Wichtiger ist, dass sich die Geschwindigkeit linear ändert, a also konstant ist. Wäre v₂ < v₁ (wenn Geschwindigkeit gemeint ist, wird das ,v’ üblicherweise klein geschrieben) so wäre a negativ, was bedeutet, dass ihre Richtung der von v entgegengesetzt wäre (das ist bei Reibungskräften grundsätzlich der Fall).
In einem t-v-Diagramm schließen die Vertikalen t=t₁, t=t₂, die t-Achse und die v(t)- Gerade ein Trapez ein, das man sich aus einem Rechteck der Breite Δt=t₂–t₁ und der Höhe v₁ und einem Dreieck derselben Breite und der Höhe Δv=v₂–v₁ zusammengesetzt denken kann.
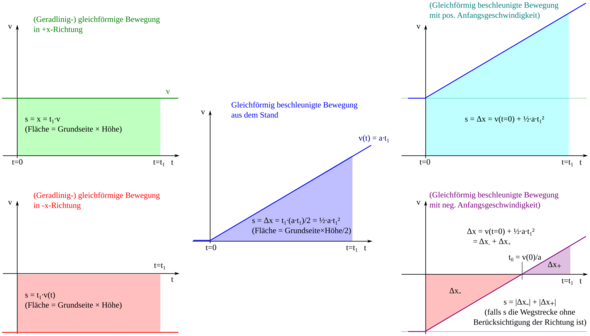
Die Frage ist nun: Was ist s? Das ist die Fläche des Trapezes
s = Δt·v₁+½Δt·Δv = Δt·(v₁ + ½Δv) = ½Δt·(v₁ + v₂).
Das gibt Dir die Möglichkeit, nach Δt aufzulösen:
Δt = 2s/(v₁+v₂),
und
a = Δv/Δt = (v₂ + v₁)Δv/2s = ⁽(v₂² – v₁²)/2s,
wobei sich Letzteres aus der 3. Binomischen Formel ergibt.
Allerdings lässt sich a auch aus dem Energie-Ansatz ermitteln, und man kommt natürlich auf dieselbe Gleichung für a, übrigens ohne Umweg über Δt.
Mit der Masse m des Körpers hat dieser nämlich bei t₁ die kinetische Energie ½mv₁² und zu t₂ die kinetische Energie ½mv₂². Die Differenz ist die Arbeit, die man auch als m·a·s schreiben kann. Dabei kommt es auf den Wert von m überhaupt nicht an, denn m fällt raus.

Ich verstehe die Frage nicht. Die Fläche im Diagramm ist der zurückgelegte Weg.
Dies ist eine "gleichmäßig beschleunigte Bewegung",weil dat Auto schneller wird.
1) a=konstant nun 2 mal integrieren
2) V(t)=a*t+Vo hier ist bei t=0=v0=V1=15 m/s
3) S(t)=1/2*a*t^2+V1*t+So hier bei t=0 ist So=0
4) S(t)=125 m
5) V2=V1+a*t ergibt t=(V2-V1)/a
5 in 3
S(t)=1/2*(V2-V1)^2/a+V1*(V2-V1)/a
S(t)=1/(a*2)*(V2-V1)^2+1/a*(V2*V1-V1^2)
a=(1/2*(V2-V1)^2+V2*V1-V1^2)/S(t)
a=(0,5*(28-15)^2+28*15-15^2)/125m=2,236 m/s^2
Einheitenkontrolle: (m/s+m/s)^2=m^2/s^2 und m/s*m/s=m^2/s^2 und (m/s)^2=m^2/s^s
oben also (m^2/s^2)/(m/1)=m/s^2
Nach der Einheitenkontrolle ist die Formel richtig,da als Einheit m/s^2 herauskommen muß
Prüfe auf Rechen- u. Tippfehler.
es gelten
s = 0,5 * a * t² + v0 * t
und
v = a * t + v0
umstellen, einsetzen und ein wenig umformen erhält man
a = (0,5 * (v - v0)² + v0 (v - v0)) / s
a = 2,236 m / s²
Du kannst mit der mittleren Geschwindigkeit rechnen. Damit bekommst du aus der Strecke s die Zeit und damit dann auch die Beschleunigung a. Probier das mal aus.
anzuwendende Formeln
s = a/2 • t² und a = delta v / t
Sicher?
das würde zu
s = delta v / ( 2 t ) * t ² = delta v * t / 2 führen
umgestellt
t = 2 * s / delta v = 2 * 125 m / 13 m / s = 19,23 Sekunden
in 19,23 Sekunden mit 15 m / s legt man jedoch schon einen Weg von 288 m zurück.
Wie kann man also von den 15 m / s noch beschleunigen und dann weniger als die Hälfte des Weges zurückgelegt haben?
Du solltest mit einem v - t Diagramm die Situation einmal aufzeichnen.
Die Fläche unter dem Graphen ist der Weg, der sich aus v1 • t und a/2 • t addiert
meine Frage wäre : wie kann man bei der gleich-beschleunigten Bewegung auf den Weg schließen, ohne auf die Fläche zurückzugreifen , auch nicht auf v = a*t