Basis eines Dreiecks anhand Winkel und Umfang berechnen?
Hallo.
Mein Lehrer hat uns ein Arbeitsblatt zum Sinus und Cosinus gegeben.
Bei der einen Textaufgabe:
"Ein gleichschenkliges Dreieck hat einen Spitzenwinkel von 30 Grad und einen Umfang von 30 cm. Wie lang ist die Basis dieses Dreiecks?"
komme ich allerdings nicht weiter... Ich verstehe nicht wie ich die Seitenlängen nur anhand der Winkel und des Umfangs berechnen soll...
Das Ergebnis, das er dazu geschrieben hat, ist 6,2 cm.
Wie sollte ich vorgehen?
Danke im Voraus!
3 Antworten
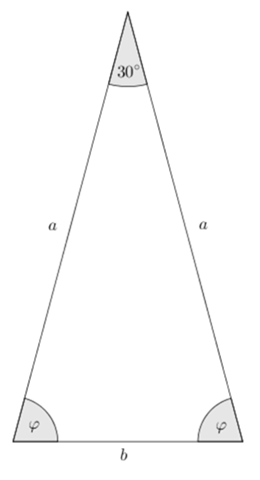
Als Erstes könnte man eine Skizze anfertigen, damit man einen besseren Überblick über die Situation bekommt.
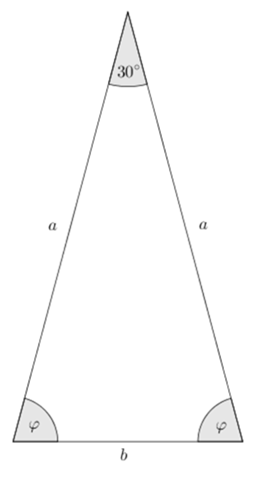
Ich habe die Innenwinkel an der Basis mit φ bezeichnet, die Länge der Basis mit b bezeichnet und die Länge der Schenkel mit a bezeichnet.
============
Mögliche Vorgehensweise:
- Berechne den Winkel φ.
- Du hast den Umfang gegeben, den du mit Hilfe von a und b ausdrücken kannst. Verwende den Sinussatz, um eine zweite Gleichung zu erhalten.
- Du hast dann zwei Gleichungen mit zwei Unbekannten a, b. Löse das Gleichungssystem, um a und b zu erhalten.
============
Ausführlich:
Neben dem 30°-Winkel an der Spitze ist bekannt, dass der Umfang 30 cm beträgt, also dass 2a + b = 30 cm ist.
Nun reicht die eine Gleichung 2a + b = 30 cm nicht aus, um daraus a und b berechnen zu können. Man braucht noch eine weitere Gleichung, in der a oder b (oder beides) vorkommt.
Zunächst einmal kann man jedoch, die zunächst unbekannten Innenwinkel φ über die Innenwinkelsumme von Dreiecken berechnen ...
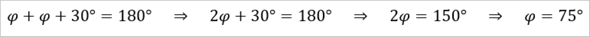
Nun kann man mit dem Sinussatz die folgende Gleichung aufstellen ...
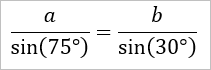
Nun hat man ein Gleichungsystem mit zwei Gleichungen und zwei Unbekannten a, b ...
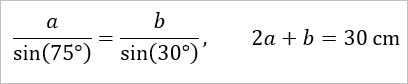
Um dieses Gleichungsystem zu lösen, kann man eine Gleichung nach einer Unbekannten auflösen ...

Das kann man dann in die andere Gleichung einsetzen, so dass man eine Gleichung hat, die nur noch von einer Unbekannten abhängt, nach der man dann auflösen kann ...

Damit hat man nun a berechnet. Man kann das nun beispielsweise in die bereits nach b aufgelöste Gleichung b = sin(30°)/sin(75°) ⋅ a einsetzen, um b zu berechnen ...
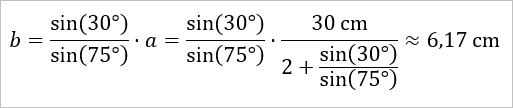
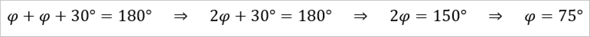
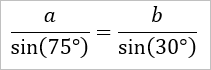
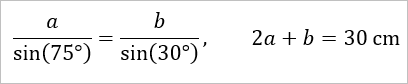


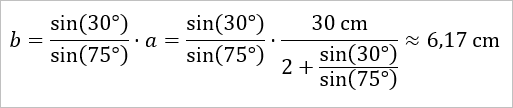
Die Längen kann man übrigens auch exakt als ...
a = (√(2) + √(6))/(1 + √(2) + √(6)) ⋅ 15 cm
b = 1/(1 + √(2) + √(6)) ⋅ 30 cm
... angeben, wenn man für sin(30°) bzw. sin(75°) die exakten Werte mit Hilfe von Wurzelausdrücken umschreibt. Allerdings sollten wohl die gerundeten Ergebnisse ...
a ≈ 11,92 cm
b ≈ 6,17 cm
... für diese Aufgabe ausreichen.
Ja, man kann die Aufgabe auch ohne Sinussatz lösen.
Idee: Unterteile das gleichschenklige Dreieck in zwei rechtwinklige Dreiecke, so dass der 30°-Winkel an der Spitze in zwei 15°-Winkel unterteilt wird. Bzgl. dem 15° ist in einem solchen rechtwinkligen Dreieck dann b/2 die Länge der Gegenkathete und a die Länge der Hypotenuse.
[Sinus = Gegenkathete/Hypotenuse]
Hier ein kompletter Lösungsvorschlag: https://www.dropbox.com/s/vdtv5ns9awjn59h/glsk.pdf?dl=0
Das entspricht auch der Vorgehensweise, wie sie von Gummipunkt und Halswirbelstrom bereits vorgeschlagen wurde.
Du kannst 2 Gleichungen aufstellen, eine über den Umfang des Dreiecks und eine mittels Winkelfunktion, erkennbar, wenn Du die Höhe auf Seite c einzeichnest. Das sollte weiterhelfen.
Wie genau die Höhe auf Seite c einzeichnen? Das Dreieck umdrehen quasi?
Die Grundseite des Dreiecks ist die Seite c. Gegenüber von c liegt Dreieckspunkt C mit dem Winkel 30°. Die Höhe steht senkrecht auf c und teilt das Dreieck in 2 rechtwinklige Dreiecke. Wenn die anderen beiden gleichlangen Dreiecksseiten mit a bezeichnet werden, gilt (c/2)/a = sin (15°). Das ist eine von den beiden Gleichungen. Die zweite Gleichung bildest Du über den Umfang: a + a + c = 30.
Teile das Dreieck mal in zwei gleiche Hälften, die dann jeweils rechtwinklige Dreiecke sind. Mit den üblichen Formeln müsstest du dann weiterkommen können.
Wenn a=b und a+b+c=30 - wie kannst Du dann wohl c in Abhängigkeit von a ausdrücken?
Aber man hat doch trotzdem keine genauen Seitenlängen gegeben?
Du weißt aber, dass der Winkel bei C 30° beträgt. Von dem Teildreieck (z.B. die rechte Hälfte) also 15°. Über die Sinusformel kannst du jetzt das Verhältnis von a und 1/2 c ausrechnen.
Du weißt auch, dass a+1/2c die Hälfte des Gesamtumfangs ist. Damit hast du alle Daten, die du brauchst, um die Basis c auszurechnen.
Gäbe es eine Möglichkeit die Aufgabe auch ohne Sinussatz zu berechnen? (also nur Sinus, Cosinus und Tangens) Wir sind in Mathe noch nicht so weit und mein Lehrer meinte mir heute, die Aufgabe sei auch ohne Sinussatz lösbar allerdings kommen meine Freundin und ich so wirklich nicht weiter... nicht mal ansatzweise!