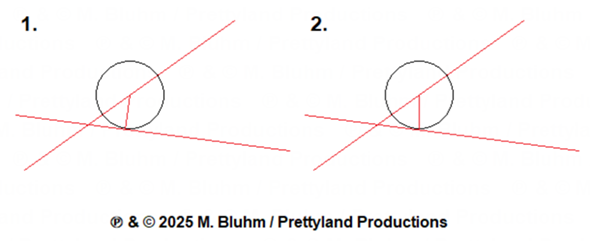
An die Mathematiker: wieso ist das so?
Wenn ich so einen Kreis habe dessen Mittelpunkt auf einem der Geraden so liegt, dass der Rand des Kreises die andere Gerade berührt, dann gibt es ja wie dort eingezeichnet einen rechten Winkel aber wieso ? Gibt es da eine intuitive Hinleitung?

3 Antworten
„Berühren“ heisst ja gerade, dass die entsprechende Tangente senkrecht auf den eingezeichneten Kreisradius steht. Wenn es kein rechter Winkel wäre, würde die Gerade den Kreis schneiden - auf einer Seite würde die Gerade dann innerhalb des Kreises verlaufen…
Die Eigenheit des Kreises ist ja, dass jeder Punkt denselben Abstand zum Mittelpunkt hat. Somit hat die Kurve, die die Kreisperipherie in einem Punkt auf ihr beschreibt, relativ zu dessen Verbindung zum Mittelpunkt immer einen Hochpunkt. Und in einem Hochpunkt gibt es immer eine senkrechte bzw. horizontale Tangente.
Du kannst einen rechten Winkel von der Geraden zum Kreismittelpunkt zeichnen (1.). Wenn Du aber eine Senkrechte aus dem Mittelpunkt zeichnest (2.) und die untere Linie ist nicht waagerecht, dann gibt's auch keinen rechten Winkel.