Zauberwürfel als Gruppe?
Moin Leute ich muss die Gruppeneigensschaften an einem Zauberwürfel erkunden.
- Die Abgeschlossenheit gilt das ist sehr logisch
- Neutrales Element ist vorhanden die 0 drehnung also wenn ich gar nicht drehe oder die 360 drehung
- Inverses Element ist vorhanden denn ich kann jede drehung durch eine gegendrehung rückgänging machen
Jetzt habe ich mein problem mit der assoziativität. Kann mir bitte jemand anhand des würfel so einfach wie möglich erklären wieso hier die assoziativität gilt. am besten so erklären dass ich es quasi am würfel mir vor meinen augen visaulisieren kann.
Vielen dank !
mfg
1 Antwort

Drehungen sind Permutationen der einzelnen Seitenflächen und als solche Teil der symmetrischen Gruppe, die aus allen möglichen Permutationen der Seitenflächen besteht. Die Hintereinanderausführung von Drehungen ist eine Komposition (Verkettung) von Abbildungen. Und die Komposition ist assoziativ
Beispiel: Diedergruppe beim Dreieck
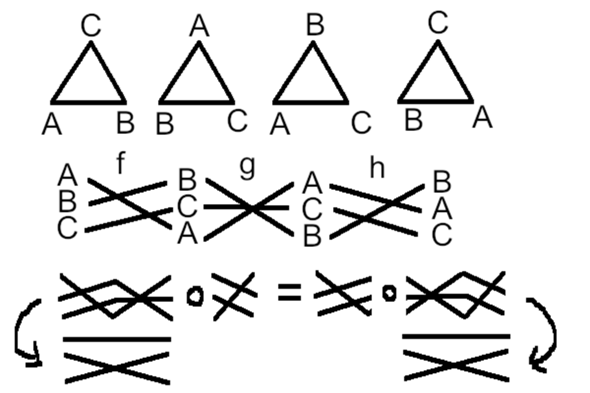
Beim Zauberwürfel kann man die 9 mal 6 Aufkleber (bei einem Würfel mit Aufklebern) vertauschen, wobei nur eine Untergruppe aller Permutationen möglich ist. Zur Veranschaulichung eine Permutationsgruppe, wo drei Ecken vertauscht werden. Hier wird das Dreieck erst im Uhrzeigersinn gedreht, dann werden Vorder- und Rückseite vertauscht, wobei der rechte untere Punkt fixiert ist, dann wird gegen den Uhrzeigersinn gedreht.
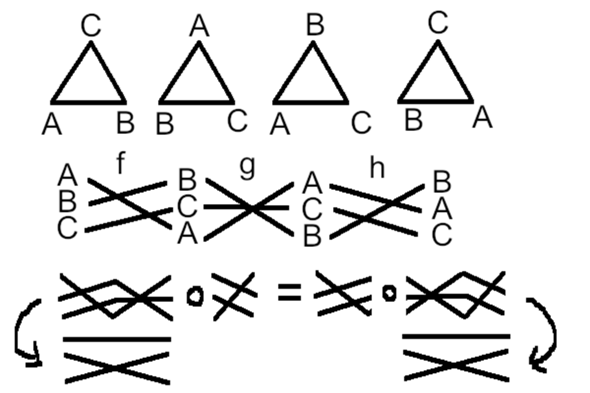
Eine solche Drehung kann man als Abbildung darstellen. f wäre die Abbildung, die 1 auf 3, 2 auf 1 und 3 auf 2 abbildet. Wenn man alle drei Abbildungen zusammensetzt, erhält man die Abbildung die 1 auf 2, 2 auf 1 und 3 auf 3 abbildet. Dabei ist es egal, ob man zunächst f ∘ g zusammensetzt oder erst g ∘ h. Das ist so wie mit Vektoren als Pfeile. Von den drei Pfeilen ist es egal, welche zwei ich zuerst zusammenfasse. Die Reihenfolge darf hier allerdings nicht vertauscht werden. Beim Zauberwürfel wäre für jeden Stein oder Aufkleber egal, ob er von 1 nach 2 nach 3 nach 4, von 1 nach 3 nach 4, indem ich "von 1 nach 2 nach 3" zusammenfasse, oder von 1 nach 2 nach 4 geschickt wird, indem ich "von 2 nach 3 nach 4" zusammenfasse.
Beim Zauberwürfel sind die einzelnen Drehungen nur die erzeugenden Elemente der Gruppe. Eine Folge von Drehungen wird beim Zauberwürfel Algorithmus genannt. Es gibt ja solche Folgen, die z.B. drei Ecken oder drei Kanten vertauschen. Wenn ich jetzt die Folge F R U habe, könnte ich F R zu einem Algorithmus zusammenfassen und dann U ausführen oder ich könnte F ausführen und R und U zusammen als einen Algorithmus betrachten. Es werden in jedem Fall F, R und U hintereinander ausgeführt. Und wenn es eine andere Folge mit der selben Wirkung wie F R gibt und danach U ausgeführt wird, wäre die Wirkung insgesamt auch die gleiche wie wenn F R U ausgeführt wird und das wäre wiederum äquivalent dazu, wenn zuerst F ausgeführt wird und danach eine Folge mit der selben Wirkung wie R U.

Leider verstehe ich das noch nicht ganz :/ könntest du das vielleicht noch mal bisschen verständlicher erklären bitte :)?