Wie kann ich anhand eines Graphen von einer Hyperbel den funktionsgraphen ablesen?
Wenn ich die hyperbel im koordinatensystem hab wie kann ich dann die formel einleiten zu der grundformel? die ja lautet a•(x-d)²+e
was muss ich tun/ablesen jnd wo in die formel einsetzen damit ich die komplette formel rauskriege?
4 Antworten
f(x) = a•(x-d)²+e
ist die Scheitelpunktform einer Parabel. Mit einer Hyperbel hat das nichts zu tun.
Zunächst liest du im Koordinatensystem den Scheitelpunkt ab: S(d/e)
Fehlt nur noch a. Das Vorzeichen erkennst du daran, ob die Parabel nach oben offen ist: +
oder nach unten offen ist: -
Dann fehlt noch der Wert des Streckungsfaktors a. Da denkst du dir ein neues Koordinatensystem, dessen Ursprung im Scheitelpunkt liegt und guckst, welcher y-Wert bei x = 1 abzulesen ist. Das ist dann der Wert von a.
Beispiel:
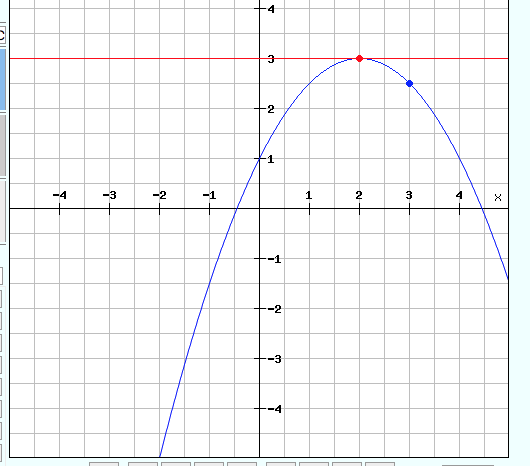
Der rote Punkt ist der Scheitelpunkt:
S(2/3), also:
f(x) = a(x - 2)^2 + 3
Die rote Linie ist das gedachte neue Koordinatensystem. Da gehst du vom Scheitelpunkt um 1 nach rechts und liest ab, was bezogen auf die rote Linie der y.Wert wäre: -0,5. Das ist dein a.
Also lautet die Funktionsgleichung:
f(x) = -0,5(x - 2)^2 + 3
Du meinst sicher "Parabel", da dort die Scheitelpunktform y=a(x-d)²+e lautet. "Hyperbel" nennt man u. a. die Graphen zu y=a/x...
Bei der Scheitelpunktform ist der Scheitelpunkt S bei (d|e). D. h. wenn Du die Parabel vorliegen hast, liest Du den Scheitelpunkt ab und setzt dessen x-Wert für d ein und den y-Wert für e. Den Streckungsfaktor a erhältst Du, indem Du vom Scheitelpunkt eine Einheit nach links oder rechts gehst. Das a ist dann der Wert, den Du nun in y-Richtung gehen musst, um wieder auf der Parabel zu landen.
Hyperbel allg.:
f(x) = (a / (x + b)) + c
a = Streckung / Stauchung / Spiegelung
b = Verschiebung in x-Richtung
c = Verschiebung in y-Richtung
Das sieht eher nach Parabeln aus.