Wie berechne ich ob der Punkt P(-2/3) auf der verschobenen Normalparabel liegt?
Hallo,
Ich sitze gerade an so einer Aufgabe und verstehe es nicht. Ich soll rechnerisch untersuchen ob der Punkt P(-2/3) auf der verschobenen Normalparabel mit dem Scheitelpunkt S liegt. Und eine Funktionsgleichung angeben
a) S(-3/2). b) S (1/-3). c) S (0/-2)
Vielen Dank im Voraus für eure Antworten.

3 Antworten
a)
in die Scheitelpunktsform
y = ( x - xs )² + ys den S einsetzen und auch (-2/3)
.
y = ( x - - 3 ) + 2
y = ( x + 3 )² + 2
jetzt -2/3
ist 3 = ( -2 + 3 )² + 3 ?
3 = (1)² + 3
3 nicht gleich 4
Nein , liegt nicht
Ab 3=(-2+3)^2 + 3 hast du einen Fehler! Es muss dort 3=(-2+3)^2+2 heißen und es kommt 3=3 raus. Der Punkt P liegt auf der Funktion f(x)= (x+3)^2 + 2
mit -2/3 ist ein Zahlendreher gemeint. Aber du hast ja sicher das andersrum eingesetzt und bis zu welchem Ergebnis gekommen ?
Guggst du hier für die Scheitelpunktform
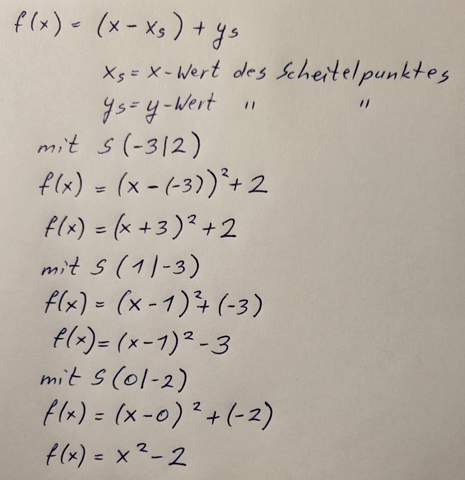
Und ob der Punkt P auf der Funktion liegt, überprüft man, indem man den x-Wert von P für alle x einsetzt. Und wenn sich als Funktionswert der y-Wert von P ergibt, liegt P auf dem Graphen der Funktion, ansonsten eben nicht!
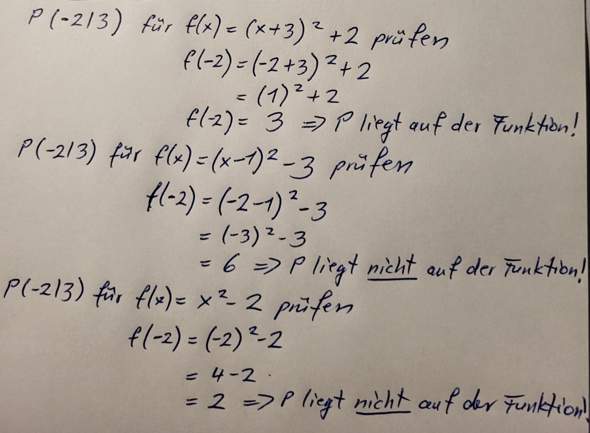
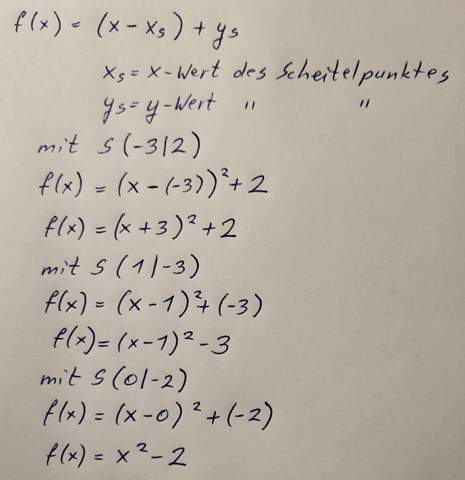
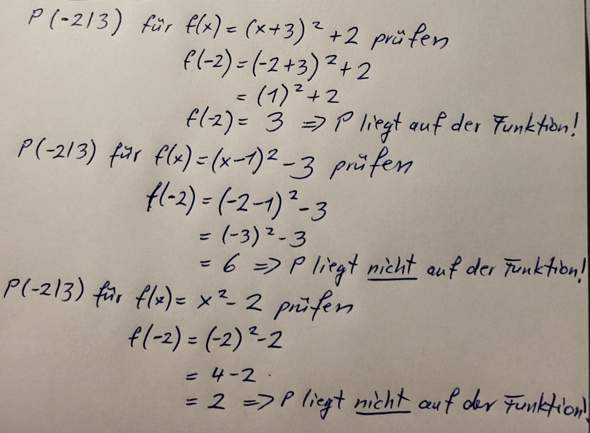
Für die funktionsgleichung musst du nur in die scheitelpunkt form einsetzen. und überprüfen tust du, in dem du für x -2 einsetzt und schaust, ob 2 haraus kommt
Was ist mit -2/3 gemeint? Der Scheitelpunkt ist bei der a -3/2