Funktionsgleichung einer Parabel berechnen?
Hi,
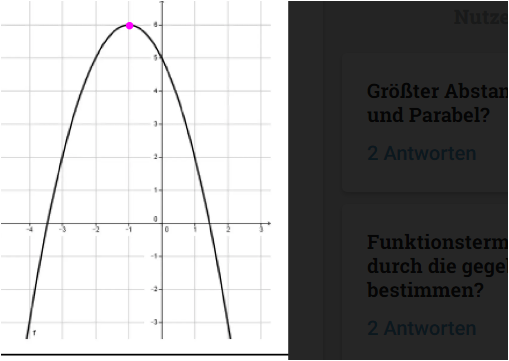
ich habe hier so eine Parabel und in der Aufgabenstellung steht,: ,,Berechne die Normalform und die Shnittpunktfrom dieser Parabel" und ganz ehrlich, ich sitze seit mehreren Stunden an dieser Aufgabe und bin komplett verzweifelt.😶 Kann mir jemand bitte die Vorgehensweise bei solch einer Aufgabe erklären? Vielen Dank im voraus 😊

2 Antworten
das man so einsetzen kann , wie es gleich passiert , muss man wissen

da ist der Scheitelpunkt . Bei (-1/6)
y = - ( x + - 1)² + 6 ist der Ansatz .................minus vorne , weil nach unten geöffnet
y = (x-1)² + 6
y = -x² + 2x + 4 ...................Das ist die Normalform
nun
0 = -x² + 2x + 4 .........................mal -1
0 = x² - 2x - 4 .............................pq
x1 2 = +1 + - wurzel(1 - - 4)
x1 = 1 + w(5)
x2 = 1 - w(5)
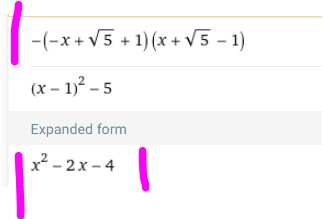
y = - ( x - (1+w(5) ) * ( x - ( 1-w(5) ) ist die Schnittstellenform
und dieses Produkt ist , vielleicht überraschenderweise , dasselbe wie oben

Wenn der Scheitelpunkt einer Parabel bei (x0|y0) liegt, so kannst du die Parabel schreiben als
p(x) = a*(x - x0)² + y0
Den Scheitelpunkt kannst du einfach ablesen. Weiter kannst du bei x1 = 1 einen y-Wert y1 ablesen. Setze dann
p(x1) = y1
und löse nach a auf. Die Normalform erhältst du durch Ausmultiplizieren des Binoms und zusammen fassen. Die Schnittstellenform (oder Nullstellenform) erhältst du indem du mit der Mitternachtsformel die Nullstellen x2 und x3 ausrechnest,
p(x) = a*(x - x2)(x - x3).
Sorry aber das ist etwas zu grob 🙁