Welcher Punkt der Funktion hat den geringsten Abstand zum Ursprung?
Unzwar plagt mich seit Wochen eine Aufgabe aus dem Mathe Grundkurs. Konkret lautet die Aufgabenstellung:
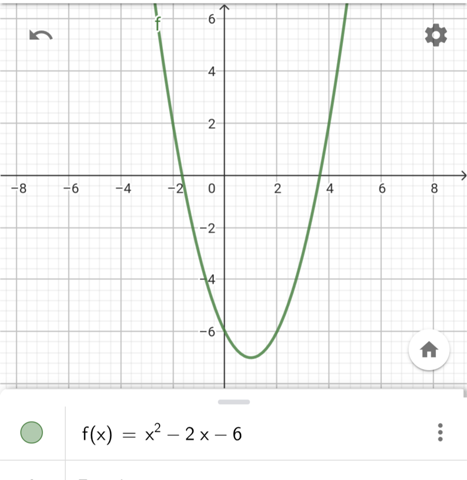
"Gegeben ist die Funktion f durch f(x)=x²-2x-6. Welcher Punkt des Graphen von f hat den kleinsten Abstand vom Ursprung?"
Ich habe schon einiges versucht, bin jedoch nie auf realistische Ergebnisse gekommen. Irgendwelche Magie mit Kreisen und Geraden und Gleichungen habe ich ausprobiert.
Es muss jedoch einfacher sein als ich denke, gerade wenn ich die anderen Aufgaben betrachte.
Es handelt sich nicht um eine Hausaufgabe. Ich möchte bloß ruhig schlafen und die Stimmen in meinem Kopf besänftigen. Ich danke ich voraus.
4 Antworten
Der Abstand d kann mittels Pythagoras bestimmt werden:
d² = Δy² + Δx²
Da der Abstand zum Koordinatenursprung gesucht wird, gilt:
d² = y² + x²
y² kann eingesetzt werden, damit eine Variable übrig bleibt:
d² = (x² - 2x - 6)² + x²
Die Wurzel kann man sich sparen, da der kürzeste Abstand auch das kürzeste Quadrat des Abstandes hat:
d(x) = (x² - 2x - 6)² + x²
d'(x) = 4x³ - 12x² - 14x + 24
Ableitung gleich Null setzen und x bestimmen führt zu:
x = -1,5871...
y = -0,3069...
d = 1,6165...
Danke sehr für die verständliche Antwort. Von den vorgeschlagenen Varianten war diese für mich am einfachsten zu erklären. Auch wenn ich nicht genau verstanden habe warum wir die Wurzel weg lassen. Jedenfalls haben ich und meine Lehrerin es mit Wurzel gemacht. Wahrscheinlich um es für die anderen Schüler auch verständlich zu halten.
Der Punkt P(x; f(x)) hat vom Ursprung (0; 0) den Abstand d(x)=√( (x)² + f(x)² ). Gesucht ist das absolute Minimum von d, – also d(x) ableiten, die Nullstellen von d' bestimmen und dann untersuchen, für welche davon d(x) am kleinsten ist. Da √x streng monoton steigt, kannst Du der Einfachheit halber auch die Nullstellen von d²(x) = (x)² + f(x)² berechnen. Das ist ein Polynom 4. Grades. Für die Nullstellen musst Du also eine Gleichung 3. Grades lösen, und dem Schaubild nach sind alle 3 Lösungen ziemlich krumm. Mit Raten kommst Du da nicht weit und die Lösungsformel geht weit über den Schulstoff hinaus. Du brauchst also ein Hilfsmittel wie das Newtonverfahren oder gleich WolframAlpha.
Methode 2:Im gesuchten Punkt geht die Kurvennormale durch den Ursprung. Bestimme also für beliebiges x₀ die Normale n(x)=mx+b und schau dann, für welche x₀ das konstante Glied b verschwindet. Ich vermute stark, dass Du auf dieselbe Gleichung 3. Grades wie oben stösst.
Methode 3:Lege einen Kreis mit Radius r um den Ursprung (x²+y²=r²) und schneide ihn mit f. Für welches r hat x² + f(x)² = r² genau eine Lösung?
Links steht schon wieder d², also ein Polynom 4. Grades, und ich sehe keine Abkürzung, die die Suche nach den Tiefpunkten umgeht.
Schade eigentlich. Vielleicht gibt es ja eine elegante Methode 4, aber angesichts des Ergebnisses (d≈1,6165 bei x≈−1,5871) steige ich hier aus.
Du hast f(x)=y
Nun kannst du mit Phythagoras den Abstand von einem Punkt auf der Kurve zum Ursprung mit
x**2+y**2 = Abstand**2
bestimmen.
Dh. man kann eine Funktion machen die den Abstand als Funktionswert mit x als Variabel hat. Nun schaue wo das Minimum dieser Kurve ist, dort hast du den minimalen Abstand.
Der Ursprung ist ja bekanntlich (0/0). Am Graph kannst du einfach ablesen, welcher Punkt der Funktion am nähsten beim Ursprung ist.
Gleichungen oder Formeln brauchst du hierfür nicht.