Was ist die allgemeine Formel für Permutationen in dieser Aufgabe?
Guten Abend,
im Chemie Unterricht ergab sich ein Problem, es ist jedoch kein Chemisches als vielmehr ein Mathematisches.
Man betrachte eine Menge n an Dingen (Bsp. a,b,c), welche miteinander in k Stellen kombiniert werden können. Wichtig dabei ist, dass eine Rotation (Bsp. abba statt baab) doppelt zählt. Gesucht ist die Anzahl an Kombinationen, wobei irgendwo in allen ks immer jedes n vorhanden sein muss. So wäre die Lösung 8 für 2 Dinge (n) an 3 Stellen (k), also einfach n^k nicht korrekt, da aaa und bbb keine validen Ergebnisse sind. Die Frage ist nun: Gibt es eine allgemeine Lösungsformel für beliebige n und k und wenn ja, wie lautet sie. Alternativ wäre natürlich ein Informatikprogramm zur Berechnung sehr hilfreich.
Vielen Dank im Vorraus
PS: Sollte sich jemand für den Ursprung des Problems interessieren kann ich das natürlich nachreichen.
2 Antworten
das sind die Standardformeln

die Lösung 8 für 2 Dinge (n) an 3 Stellen
da würde ich erstmal sagen : n = 3 , und k_2 besteht aus k1 = 1 und k2 = 2
abb
bab
bba
baa
aba
aab..........................wären das alle validen ?
PmW passt , wenn man k1 = 1 und k2 = 1 setzen würde
Das passt ,denn die Grundmenge ist ja { a, b }
Durch Wiederholung entsteht bei drei Plätzen mehr als ein a ( b ) . Und weil jedes Element ausgewählt werden muss , sind aaa und bbb ausgeschlossen.

du solltest mal ein Beispiel geben
wenn bei 4 und 3 36 Perm entstehen soll , kimmt eigentlich nur KmWdh in Frage , denn nur dort würde im Zähler eine Zahl stehen, die groß genug ist , um auf 36 zu kommen
aber 6!/3!*3! =
6*5*4/6 = 20 reicht auch nicht zu 36
.
PS : 36 scheint mir auch zu groß , wenn in jedem Vierer a , b und c vorkommen müssen.
Alles klar, ein Beispiel ist nicht schlecht. Wie gesagt ergeben sich bei Vier Stellen und drei Objekten 36 Lösungen. aabc aacb abac abca abcc abbc abcb acbc accb acab acbb acba das sind 12 Lösungen, welche mal drei genommen werden müssen wegen der drei Variablen. Mein Versuch für eine Formel war n^k-n(n-1)^k aber das führt zu 33 Ergebnissen (ich weiss nicht warum). 3^4–3(3–1)^4
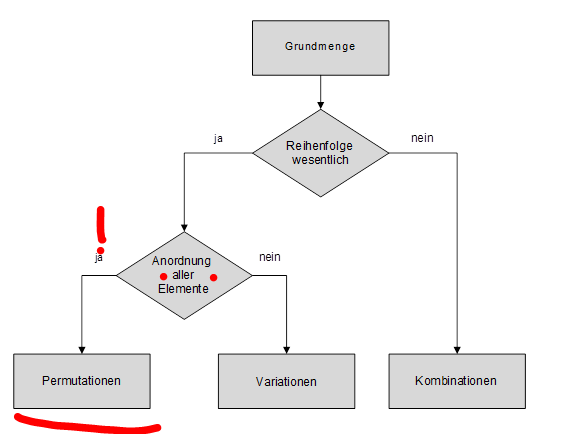
Meinst du vielleicht eine Permutation mit Wiederholung,
das ist eine Anordnung von n Objekten bei der die Reihenfolge eine Rolle spielt und Elemente mehrfach vorkommen können also ununterscheidbar sind:
Die Anzahl der möglichen Anordnungen also der möglichen Permutationen beträgt dann:
n! / (k_1*......*k_s)
Dabei ist k_i die Anzahl der ununterscheidbaren Objekte in der i-ten Gruppe von insgesamt s Gruppen mit ununterscheidbaren Objekten und n die Anzahl der Objekte insgesamt
Siehe:
Danke für diese umfangreiche und gute Antwort. Ich habe leider die Befürchtung, dass das nicht das volle Problem beschreibt. Die Formel funktioniert, soweit ich das ersehen kann, zum Beispiel nicht, wenn es drei Objekte an Vier verschiedenen Stellen sind. Das Ergebnis wären nämlich eigentlich 36 Permutationen. Es handelt sich ja auch nicht um Gruppen sondern um einzigartige Objekte.