Wahrscheinlichkeit Problem
Hallo, ich habe folgende Aufgabe: 60% aller Jugendlich hören gerne Rockmusik. 30% der Jugendlichen sind und hören nicht gerne Rockmusik, 40% sind männlich und hören gerne Rockmusik.
Nun soll ich ein Baumdiagramm aufstellen und vers. Fragen beantworten. Mein Problem liegt allerdings schon im ersten Punkt.
Ich habe mir erstmal mit Hilfe dem Satz der totalen Wahrscheinlichkeit die Restlichen Schnittmengenwahrscheinlichenkeiten errechnet.
Legende: M männlich
W weiblich
R mag Rock
/R mag Rock nicht
W geschnitten R = 0,2
W geschnitten /R = 0,3
M geschnitten R = 0,4
M geschnitten /R = 0,1
Nun habe ich zwar die Schnittmengen, aber die Wahrscheinlichkeiten der einzelnen Äste des Baumes habe ich nicht. Wie mache ich das? Mit einer 4 Felder-Tafel komme ich auch nicht weiter. weil hier würde folgendes rauskommen:
M = 0,5 W = 0,5 R = 0,6 /R = 0,4
Irgendwie wäre das zu einfach und passt einfach nicht.
Synapse22 Danke!!
3 Antworten
Versuch das ganze doch als Zufallsexperiment "durchzuführen", also bspw. indem du dir die Fragestellungen als Urnen mit verschiedenen Kugeln oder als Glücksräder mit verschieden großen Bereichen vorstellst. Dann kan man das "Experiment" so gestalten: Zuerst wird mit einer 50/50-Glücksrad herausgedunden, ob es sich um W oder M handelt. Dann gibt es ein spezielles W- Glücksrad, das mit 40% Rock und mit 60% "nicht Rock" anzeigt. (entsprechend also 0,2 bzw. 0,3, die die Gruppen am Gesamtanteil haben). Entsprechend gibt es ein M-Glücksrad mit 080% und 20%-Einteilung. Übertragen in deinem Baum wäre das also:
erster Zweig: 0,5 M und 0,5 W (Entsprechend 0,4+0,1=0,5 und 0,2+0,3=0,5) zweite Verzewigung: Bei M gehen 0,8 auf R und 0,2 auf /R, Von W gehen 0,4 auf R und 0,6 auf /R. Man kann ja dann die Probe machen: M und R wäre z.B. dann nach der Pfadregel
0,5* 0,8=0,4 --> passt.
Prinzipell lässt sich der Baum natürlcih auch "andersrum" gestalten, indem man zuerst nach R und /R unterteilt. Das wären dann die Wahrscheinlichliekteiten 0,6( 0,4+0,2) und 0,4 (0,3+0,1). Dann geht es entsprechend weiter: Von R aus unterteilt es in M und W Vom "Gestamt-R-" Anteil sind 0,4/0,6=2/3 männlich und 0,2/0,6=1/3 weiblich. Entsprechend beim /R-Zweig: 0,1/0,4=0,25 sind M, 0,3/0,4=0,75 sind weiblich. Auch hier kann man ja zur Sicherheit wieder die Probe machen.
Hier das Baumdiagramm. In schwarz die Angaben aus dem Text. In grün deine Berechnungen . In rot die fehlenden Berecnungen in der Reihenfolge, wie du sie vornehmen kannst.

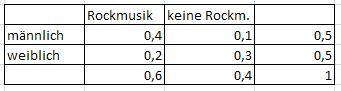
Du hast Probleme mit der Vierfeldertafel? Hier ist sie. Damit kannst du alles spielend ausrechnen.