Umwandeln in Scheitelform?

Answer 1

[mihisu]

Nutze eine binomische Formel. Evtl. musst du dafür auch eine sogenannte quadratische Ergänzung durchführen.

https://de.wikipedia.org/wiki/Quadratische_Ergänzung#Bestimmung_der_Scheitelpunktform_einer_quadratischen_Funktion

Dabei wird ein Quadrat einer passenden Zahl addiert, so dass man eine binomische Formel anwenden kann. Zum Ausgleich muss man andererseits das Quadrat dieser Zahl auch wieder subtrahieren, um insgesamt den Wert nicht zu verändern.

============

Lösungsvorschläge mit relativ ausführlicher Rechnung (aber ohne weitere Kommentare zur Rechnung)...

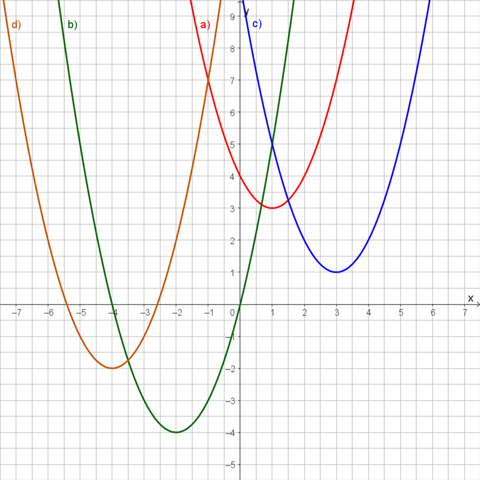
Zu a):

$y=x^2-2x+4$

$y=x^2-2\cdot x\cdot 1+4$

$y=x^2-2\cdot x\cdot 1+1^2-1^2+4$

$y=\left(x-1\right)^2-1^2+4$

$y=\left(x-1\right)^2-1+4$

$y=\left(x-1\right)^2+3$

Zu b):

$y=x^2+4x$

$y=x^2+2\cdot x\cdot 2$

$y=x^2+2\cdot x\cdot 2+2^2-2^2$

$y=\left(x+2\right)^2-2^2$

$y=\left(x+2\right)^2-4$

Zu c):

$y=x^2-6x+10$

$y=x^2-2\cdot x\cdot 3+10$

$y=x^2-2\cdot x\cdot 3+3^2-3^2+10$

$y=\left(x-3\right)^2-3^2+10$

$y=\left(x-3\right)^2-9+10$

$y=\left(x-3\right)^2+1$

Zu d):

$y=x^2+8x+14$

$y=x^2+2\cdot x\cdot 4+14$

$y=x^2+2\cdot x\cdot 4+4^2-4^2+14$

$y=\left(x+4\right)^2-4^2+14$

$y=\left(x+4\right)^2-16+14$

$y=\left(x+4\right)^2-2$

Answer 2

[Maru1]

Das ist recht einfach. Man muss nur wissen, was mit "quadratischer Ergänzung" gemeint ist.

Erstes Beispiel:

y = x^2 - 2x +5 = (x^2 - 2x +1) + 4 = (x-1)^2 + 4

Man erhält diese Parabel, indem man die Normalparabel (mit der Gleichung y = x^2) um 1 nach rechts (in x-Richtung) und um 4 nach oben (in y-Richtung) verschiebt. Der Scheitelpunkt der Parabel liegt dann also im Punkt S(1|4).

Zweites Beispiel:

y = x^2 + 4x = (x^2 + 4x + 4) - 4 = (x+2)^2 - 4

Normalparabel um 2 nach links und um 4 nach unten verschieben. Scheitelpunkt S(-2 | -4)

https://de.wikipedia.org/wiki/Quadratische_Erg%C3%A4nzung#Bestimmung_der_Scheitelpunktform_einer_quadratischen_Funktion

Answer 3

[Rammstein53]

Hat die quadratische Gleichung keinen Faktor bei +x², ergänzt man einfach mit der Hälfte des Faktors von x zum Quadrat:

a) x² - 2x + 4   mit (2/2)² = 1² ergänzen
b) x² + 4x       mit (4/2)² = 2² ergänzen
c) x² - 6x + 10  mit (6/2)² = 3² ergänzen
d) x² + 8x + 14  mit (8/2)² = 4² ergänzen

Steht bei x² ein Faktor a (also auch a = -1), dann klammert man diesen Faktor einfach aus. Aber das nur am Rande.

a) x² - 2x + 1² - 1² + 4

b) x² + 4x + 2² - 2²

c) x² - 6x + 3² - 3² + 10

d) x² + 8x + 4² - 4² + 14

Jetzt kann man die ersten drei Terme in einer Klammer zusammenfassen:

a) (x - 1)² - 1² + 4

b) (x + 2)² - 2²

c) (x - 3)² - 3² + 10

d) (x + 4)² - 4² + 14

Jetzt noch die Konstanten zusammenfassen:

a) (x - 1)² + 3

b) (x + 2)² - 4

c) (x - 3)² + 1

d) (x + 4)² - 2