Stetigkeit Funktionen?

Hallo,

Ich wollte fragen, wie man beweisen kann, dass eine funktion in einem Intervall ständig steigt?

PS? Angenommen ich möchte auf das Grenzverhalten einer Funktion schauen, dann schaue ich mir ja dann den höchsten exponenten an und bestimme daran das grenzverhalten.

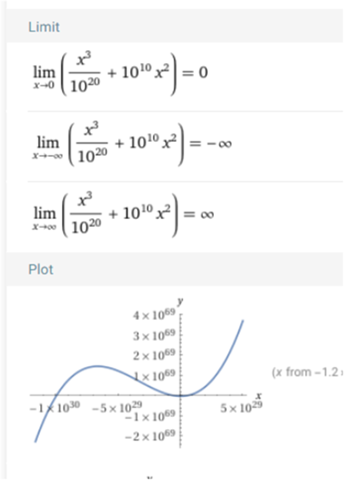
Angenommen aber, der vorfaktor eines anderen glieds ist viel größer: x³-1000000x²

Ist dann das x³ trotzdem dominanter?

Answer 1

[Uwe65527]

Ableiten und schauen, ob die 1. Ableitung >0 ist. Was differenzierbar ist, ist auch stetig.

Woher ich das weiß: Studium / Ausbildung – Dipl.-Math.

Answer 2

[aperfect10]

Ist dann das x³ trotzdem dominanzer?

Ja, ab einem bestimmten Punkt setzt sich x^3 durch, egal wie groß der Koeffizient von x^2 ist.

Answer 3

[SclauerIdiot]

Egal wie groß der Vorfaktor eines anderen glieds ist, das Glied mit dem höchsten Exponenten "setzt sich irgendwann durch".

Beispiel: x³-100000x²

X kann beliebig groß werden. X ist dann irgendwann gleichgroß wie der Vorfaktor. In diesem Fall würde stehen:

100000³-100000*100000²=

=100000*100000*100000-100000*100000*100000=

=0

Hier wären beide Glieder bereits ausgeglichen. Aber x kann noch größer werden, deswegen setzt sich ab hier das Glied mit dem höheren Exponenten durch.

Answer 4

[Halbrecht]

selbst bei 00000000000000000000000000.1 * x³ + 10^(10000000000000000000)*x²

ist der Grenzwert + bzw - unendlich

bei höheren Exponenten werden nur die Grenzwerte angegeben , die Graphik ist eine Strich