Ich sitze schon etwas länger an dieser Aufgabe und finde keine Lösung. Kann mir bitte jemand helfen?

Kann mir bitte jemand bei dieser Aufgabe behilflich sein.

LG

Answer 1

[verreisterNutzer]

Funktionsgleichung der Parabel: $f\left(x\right)=a\cdot\left(x+2\right)\cdot\left(x-2\right)$ $f\left(0\right)=\ 4\ \to\ -4\cdot a\ =\ 4\ \to a=-1\$

Damit $f\left(x\right)=-\left(x+2\right)\cdot\left(x-2\right)=-x^2+4$

Ableitung an den Nullstellen $f'\left(x\right)=-2x\ \to f'\left(-2\right)=4;\ f\left(2\right)=-4$

Damit berechnen sich die Geraden zu: $g_1\left(x\right)=4x+\ b;\ g_1\left(-2\right)\ =\ 0\ \to-8\ +\ b\ =\ 0\ \to b\ =\ 8\$ $g_2\left(x\right)=-4x+\ b;\ g_2\left(2\right)\ =\ 0\ \to-8\ +\ b\ =\ 0\ \to b\ =\ 8\$

Die Gleichungen der beiden gesuchte Geraden lauten also $g_1\left(x\right)=4x+8;\ \ g_2=-4x+8$

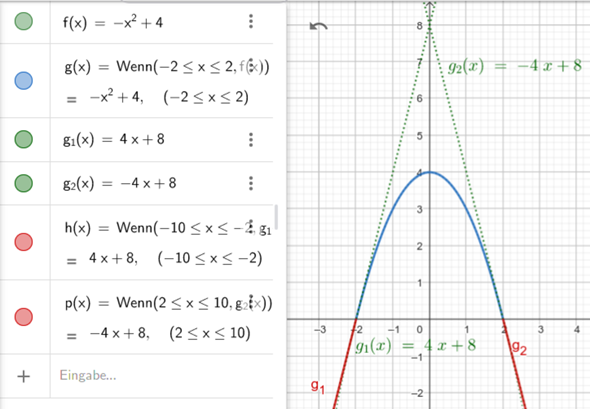
Skizze:

Answer 2

[Halbrecht]

hier ist der Ursprung

a(x-2)(x+2) = a(x² - 4) .............

für a den Punkt 0/4 nutzen
4 = a*(0²-4) = -4a
-1 = a

f(x) = -(x²-4) = -x² + 4

f'(x) = -2x
f'(-2) = +4 , +4 ist die Steigung bei (-2/0) . Diese Steigung soll auch die Gerade haben und durch den Punkt (-2/0) gehen

0 = +4*-2 + b
8 = b

y = 4x + 8 ist die Gerade

Answer 3

[Terminator333]

f(x)= -x² + 4 (dies folgt aus den gegebenen Punkten)

f'(x)=-2x

---> Fundament Gerade 1 hat Anstieg 4 (f'(-2)=4) und Gerade 2 Anstieg -4

g1(x)= 4x+8

g2(x)= -4x+8

Woher ich das weiß: Studium / Ausbildung – Mathestudent