Stabilität eines Zustandsystems?
Hallo, mir erklärt sich die Stabilität eines Systems nicht ganz, vielleicht kann mir da jemand weiterhelfen.
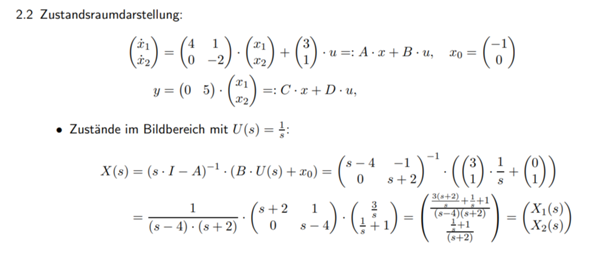
Laut Lösung ist X_1(s) instabil, soweit verständlich wegen dem Pol bei 4.
Jedoch sagt die Lösung, dass X_2(s) Stabil sei. Mein Gedanke wäre angesichts des Poles bei 0, dass dieser Grenzstabil ist. Damit wäre auch Y(s) Grenzstabil.
Lösung:
Jedoch gilt wiederum:
Anscheinend habe ich irgendwo einen Gedankenfehler, wäre nett wenn mir wer helfen könnte.
2 Antworten
Wenn man sich die Differentialgleichungen anschaut sieht man sofort, dass x1 gegen unendlich und x2 gegen einen endlichen Wert geht:
x1 wirkt positiv auf x1'(Mitkopplung), während x2 negativ auf x2' wirkt(Gegenkopplung).
Formal gesehen muss man die charakteristische Gleichung
det(s*I-A) = 0 lösen. Man erhält s=2 (Eigenwert bzgl. x1) und s=-4 (Eigenwert bzgl. x2)
Und außerdem gibt es bei dem System keinen Pol in 0.
Wenn X_2=((1/s)+1)/s+2=(s+1)/s*(s+2) ist, dann sieht man doch aber das die Nullstellen des Nennerpolynoms s=0 und s=-2 sind. Demnach haben wir einen Pol bei -2 und einen bei 0 oder irre ich mich da. Mir ist klar, dass das der Zustand dann gegen einen endlichen wert strebt. Aber es muss doch für t-> Inf x(t)=0 gelten und nicht ≠0.
Kann es sein, dass ich mir für die Stabilitätsbetrachtung von X(s) einfach nur das System an sich angucken muss, ohne Bezug auf Eingang und Startposition.
Würde für mich halt wenig Sinn machen, weil was ist wenn ich start und Eingang gerade so wähle, dass der Ausgang stabil wird z.B. durch Kürzung der Instabilen Polstellen.
Dankeschön für die Ausführliche Erklärung, hat mir gerade einen Knoten aus'm Kopf gelöst. ♥️
x_1(s) ist instabil aufgrund des Pols bei 4, das hast du richtig erkannt, Aber bei x_2(s) liegt der Pol bei 0 und das macht es stabil, nicht nur grenzstabil, Dadurch ist auch Y(s) stabil. Ich kann nicht genau sagen, wo dein Gedankenfehler liegt, aber du hast die stabilität für x_2(s) richtig interpretiert
Polstelle bei 0->Teil auf der Imaginären Achse->Grenzstabilität
X_2 ist keine Übertragungsfunktion, sondern eine Zustandsgröße und in dem Beispiel ist sie als Ausgang definiert. Die Berechnung der Polstellen für Stabilitätsuntersuchung bezieht sich auf Übertragungsfunktionen und es gilt
X_2 = G_2 * U, bzw. G_2 = X_2 / U.
Jetzt wird klar, dass dieser vermeintlicher Pol in 0 eigentlich U ist.
x(t) muss für t gegen inf nicht gegen null gegen, sondern er geht gegen seinen Ruhepunkt/Arbeitspunkt, falls stabil. Die Ableitung von x muss zu null gesetzt werden, um den Ruhepunkt zu ermitteln. Man nimmt ohne Beschränkung der Allgemeinheit an, dass der Ruhepunkt in null liegt, um die Analyse einfacher zu halten. Durch eine Koordinatentransformation kann man nämlich den Ruhepunkt nach null verschieben. Deswegen steht das so in deinem Skript, weil stillschweigend davon ausgegangen wurde, dass zuvor eine Koordinatentransformation durchgeführt wurde. Aber für dein Beispiel hat das keine Bedeutung.
Die Stabilität hängt nicht von u ab, sondern durch die Fundamentalmatrix der DGL bzw. gleichbedeutend Übertragungsmatrix im s-Bereich. Man kann zwar mittels u instabile Pole kürzen, aber falls die Anfangswerte nicht alle null sind oder eine Störfunktion in das System wirkt, dann machen sich die instabilen Pole bemerkbar und das System wird instabil.
Es gibt wie gesagt 3 Anregungen: Über den Eingang u, Anfangswerte (wirken als Dirac Impulse) und Störfunktion, falls vorhanden.