Quadratische funktion?
Kann jemand diese Frage lösen:
Gegeben ist die Funktion mit
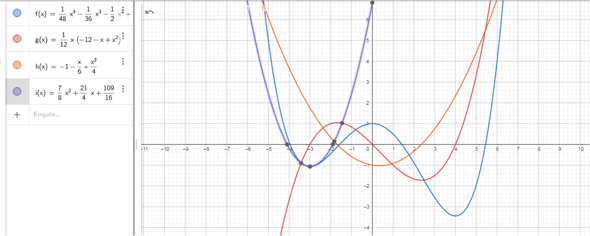
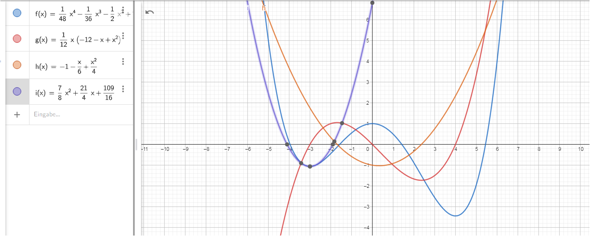
f(x)=1/48x^4 − 1/36x^3 −1/2x^2 +1.Bestimme die Gleichung einer quadratischen Funktion, die mit f im Funktionswert, der 1. Ableitung und der 2.ten Ableitng an der Stelle x0=−3 übereinstimmt.
Hinweis: Die Parabel berührt die Funktion in ihrem lokalen Minimum, d.h. die Parabel hat dort ihren Scheitelpunkt.
3 Antworten
Lösungshinweise: berechne f(-3), f´(-3) und f´´(-3) !
Die gesuchte Funktion sei g(x) = ax^2 + bx + c !
Es sind die drei Formvariablen a,b,c gesucht.
Bestimme hierzu g´(x) und g´´(x) in allgemeiner Form !
Die nötigen Gleichung um die Lösung zu finden lauten dann:
g(-3) = f(-3) ; g´(-3) = f´(-3) ; g´´(-3) = f´´(-3) ;
Auf Grund einiger Kommentare noch eine Bemerkung:
Angeblich soll es sogar Mathematiklehrer geben, die Hinweise einbauen um zu bewerten, ob die Schüler mit diesen Hinweisen korrekt umgehen. Als Fachrespizient habe ich aber keinen derartigen (möglicherweise irreführenden) Hinweis bei den von mir zu respizierenden Aufgaben meiner Kollegen gefunden. So böse scheinen die meisten Mathematiklehrer denn doch nicht zu sein.
Siehe meinen Hinweis auf die Lösung von DerRoll ! Man kann auch geschickt vorgehen. Mein Lösungsvorschlag entspricht dem Standard.
Zum Vergleich deiner Lösung
f(x) = 1/48 * x^4 -1/36 * x³ - 1/2 * x² + 1
.
::
.
f''(-3) = 7/4
f'(-3) = 0
f(-3) = -17/16
-17/16 = 9a - 3b + c ;
0 = -6a + b ;
7/4 = 2a
.
i(x) = 7/8 * x² + 21/4 * x + 109/16 ist die Parabel
Ja und was willst du nun genau wissen? Wo ist die Frage unverständlich? Berechnen den Funktionswert an der Stelle x0 = -3. Stelle dort die Scheitelpunktform mit dem freien Parameter der Streckung a auf:
g(x) = a(x + 3)^2 + f(-3)
Multipliziere aus, leite formal ab. Berechne f'(-3) und setze in g' ein. Löse nach a auf.
Eigentlich müsste hierzu aber erst noch gezeigt werden, dass f´(-3) = 0 ist.
Ja , aber in deiner Lösung verwendest du das Ergebnis bevor du es gerechnet hast.
Ich verwende eben den Hinweis. Da während der Rechnung ja genau dieser Hinweis auch bestätigt wird bin ich einfach sehr direkt vorgegangen. Wenn Hinweise gegeben sind müssen diese nach meiner Erfahrung aus dem Studium auch nicht bewiesen werden.
Im Hinweis steht aber nicht, dass der x-Wert des Scheitelpunktes der Parabel x = -3 ist. Die Parabel kann die Funktion f an mehreren Stellen schneiden oder berühren.
Das stimmt, aber wenn es mehrere Berührpunkte gäbe macht der Hinweis keinen Sinn sondern würde statt dessen auf eine völlig falsche Fährte lenken.
Und bei deiner Lösung verwendest du dass f´(-3) = 0 ist weil dies der Scheitelpunkt der Parabel ist und gibst hinterher an, dass f´(-3) berechnet werden soll. Das macht nach meiner Auffassung noch weniger Sinn.
Ich brauche dies ja um a zu bestimmen. Das f'(-3) = 0 sein muß verwende ich vorher übrigens lediglich implizit.
Das würde ich als Korrektor so nicht durchgehen lassen. Du verwendest f´(-3) = 0 ohne es vorher ausreichend begründet zu haben. Aus der Angabe oder dem Hinweis folgt es nicht direkt. Dass der Hinweis andernfalls unsinnig wäre ist keine Begründung für die mathematische Vorgehensweise. Aber dir ist ja wohl klar wie ich es gemeint habe. Gruß von Littlethought.
aber wofür braucht man den Hinweis ?