Mathe (quadratische Funktionen) ablesen?
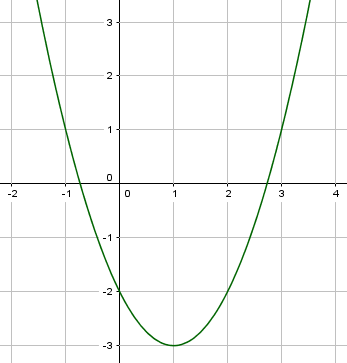
Die Funktionsgleichung wäre f(x)=(x+1)²-3 und der Scheitelpunkt ist(1/-3)
Könnte man mit den gegebenen Daten ablesen, ohne die Parabel zu sehen, in welchem Quadranten die Parabel steigt oder Fällt?
5 Antworten
man kann an der ziffer vor dem x immer die Steigung / Senkung erkennen. Wenn es - davor hat, sinkt die Parabel, wenn nicht sieht sie aus wie auf dem bild
Die Funktionsgleichung wäre f(x)=(x+1)²-3 und der Scheitelpunkt ist(1/-3)
Die Funktionsgleichung passt nicht zum Grafen/Scheitelpunkt.
f(x)=(x-1)²-3
wäre korrekt.
ja, die Funktionsgleichung reicht aus, der Scheitelpunkt alleine nicht.
allgemeine Form y=f(x)=a2*x²+a1*x+ao
Scheitelpunktform y=f(x)=a2*(x-xs)²+ys
Scheitelpunkt Ps(xs/ys) mit xs=-(a1)/(2*a2) und ys=-(a1)²/(4*a2)+ao
hier Ps(1/-3) also y=f(x)=a*(x-1)²-3 mit P(0/-2)
f(0)=-2=a*(0-1)²-3 ergibt -2=a*1-3 a=(-2+3)/1=1
y=f(x)=1*(x-1)²-3
a2=Streckungsfaktor (Formfaktor)
a2>0 Parabel nach oben offen
a2<0 Parabel nach unten offen
mit xs=1 und ys=-3 liegt der Scheitelpunkt im IV Quadranten und mit a2=a=1>0 ist die Parabel nach oben offen.
Ja, da du den Tief/Hochpunkt kennst und auch dass die Funktion zweiten Grades ist und du weißt, ob sie nach oben bzw unten offen ist.
Hier Grundinfo´s per Bild,was du mit einen Bildprogramm vergrößern kannst.
Kannst´s du vielleicht herunterladen.

