Quadratische Funktionen unterscheiden?
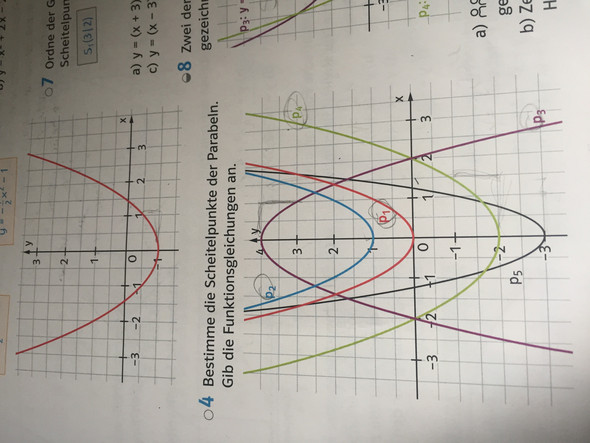
Hallo ich schreibe morgen eine Klassenarbeit und wir haben das Thema “Quadratischen Funktionen” das Problem ist da kommen Aufgaben dran wo es in einen Koordinatensystem viele Parabeln sind und ich sollte die Funktionsgleichung schreiben(sehe Bild) aber ich kann nicht unterscheiden ob die Parabel jetzt z.B Normalform,Scheitelform,quadratische Funktion (y=ax2 + c)
5 Antworten
Wenn du aus einem Graphen eine Funktion ermitteln sollst, steht ja immer oben drüber, ob du eine allgemeine Gleichung oder die Scheitelpunktform herstellen sollst
oder vielleicht zerlegt in Linearfaktoren.
Die Scheitelpunktform kannst du ablesen. Bei
f(x) = a(x - xₒ)² + yₒ
ist der Scheitelpunkt S(+xₒ| +yₒ).
x also umdrehen!
Du kannst es dann in die allgemeine Form umrechnen.
Um a zu gewinnen, setzt du irgendein Paar (x|y) in die Gleichung ein.
Die allgemeine Gleichung sieht so aus:
f(x) = ax² + bx + c
Gibt es kein bx, ist die Parabel symmetrisch zur y-Achse, aber nach oben oder unten verschoben.
Gibt es kein c, liegt eine Nullstelle im Ursprung, die andere irgendwo auf der x-Achse.
Die Parabel ist dann seitwärts verschoben.
Sind beide Nullstellen x₁ und x₂ zu sehen, kann man die Parabel auch über die Linearfaktoren berechnen.
f(x) = a (x - x₁) (x - x₂).
Für a siehe oben. (Aber nicht eine der Nullstellen nehmen!)
Der Koeffizient b ist bei allen Parabeln 0, c ist gleich
dem y-Wert bei x = 0, den kannst du ablesen.
Um a zu ermitteln, setzt du in
ax²+c
c ein und für x einen Wert ungleich 0, bei der blauen
Kurve z. B. 1:
a*1² + 1 = 2
a = 1
Usw.
Du hast zig Wege diese Aufgabe zu lösen.
Wenn du den Scheitelpunkt kennst, kannst du die Scheitelpunktform immer aufstellen.
Beispiel :
P4 :
S(0/-2)
f(x) = a*(x-0)² - 2 I P(2/0)
0 = a*(2-0)²-2
2 = 4a
1/2 = a
f(x) = 1/2*(x-0)² - 2 oder
<=> f(x)= 1/2*x² - 2
Wenn der Scheitelpunkt nicht bekannt ist, aber die Nullstellen(reelle),dann kannst du auch den Mittelwert der Nullstellen bilden.
x-Wert des Scheitelpunkt = (x_1+x_2)/(2)
Wichtig ermittle immer a !
Aus dem Graphen kann man die Scheitelpunktkoordinaten xs und ys entnehmen und damit die Scheitelpunktfunktion P(x) = a(x-xs)² + ys ermitteln.
Bei den hier gezeigten Graphen P1 bis P6 liegt der Scheitelpunkt stets auf der y.-Achse, so dass gilt xs = 0 und damit P(x) = ax² + ys.
ys ist der y-Wert des Scheitelpunkts, hier also der Achsenabschnitt auf der y-Achse. Bei P5 z.B. ist ys = -3, so dass gilt P5(x) = ax² - 3. Um auch a zu bestimmen setzt man einen Punkt der Kurve ein, z.B. A(1I-1) und erhält: -1 = a*1² - 3; ---> -1 = a - 3; ---> a = 2. Damit hat man die gesuchte Funktionsgleichung P5(x) = 2x² - 3. Der Faktor von x², nämlich a, ist hier positiv (a = 2), d.h. die Parabel ist nach oben geöffnet, wie im Bild zu sehen.
Also aus einer Grafik kann man nicht entnehmen, ob eine Parabel in Scheitelpunkt-/Normalform angegeben ist, da jede Parabel auf beide Arten gegeben sein kann. Jede Normalform kann durch quadratische Ergänzung in die Scheitelpunktform gebracht werden.