Pq-Formel mit Parametern?
Hey, ich komme bei dieser pq-Formel nicht weiter.
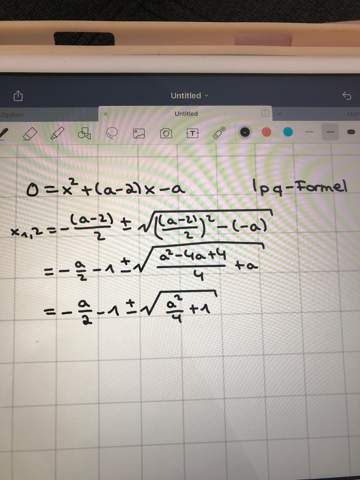
kann mir da jemand helfen?
5 Antworten
Welche Hilfe benötigst du denn genau? Auf den ersten Blick sehe ich keinen Fehler. Was da steht bedeutet dass die Gleichung für jedes a in R zwei Lösungen besitzt, da die Diskriminante immer echt größer als 0 ist.
Photomath ist eine Matheverblödungsapp, die man nur verwenden sollte wenn man das Thema ohnehin wirklich durchdrungen hat. Das ist beim Fragesteller offensichtlich noch nicht ganz der Fall.
Hm, ich nutze sie nie, habe sie, wie du siehst nur, da ich keinen Stift und Papier bei mir habe 😁, Mathematiker sind faul, wie ich sage, das hat nichts mit Verblödung zu tun, dort wird es auch einem erklärt, besser als manche es sagen/schreiben können.
Der erste Versuch ist immer holprich, beim zweiten, braucht man sowas nicht mehr.
Aus (a²/4 + 1) kannst du erst mal keine Wurzel ziehen. Es kommt dann auf das a an, weil der Radikand nicht negativ sein darf.
Nochmal, ich als Mathematiker habe auch keine Skrupel die Seite von Arndt Bruenner zu verwenden um Gleichungen oder Gleichungssysteme lösen zu lassen. Aber einem Schüler oder einer Schülerin würde ich das nie raten das zu verwenden ausser zur Lösungskontrolle.
Ich als Mathematiker, ebenso, also passt es ja :), ich nutze solche Websites nie, da ich meinen Kopf dafür habe, kann aber keine Wurzel Zeichen qm Handy eintippen, deshalb habe ich es nicht so umständlich gemacht.
Und außerdem spare ich mir die Zeit mit der Erklärung, da sie auf den sogenannten Link erklärt ist.
Ich sehe auch keinen Fehler, wenngleich ich jedoch die Lösung etwas anders geschrieben hätte. Aber das ist ja Geschackssache.
Hallo,
-(a-2)/2=-a/2+1, nicht -a/2-1.
Du kannst das Minus vor der Klammer auch so beseitigen, indem Du die Differenz in der Klammer einfach umdrehst: -(a-2)/2=(2-a)/2=1-a/2.
Merke: -(a-b)=b-a.
Ansonsten richtig.
Wenn Du möchtest, kannst Du noch unter der Wurzel 1/4 ausklammern und als 1/2 vor die Wurzel stellen, so bekommst Du als Lösungen für x
1-a/2±(1/2)*Wurzel (a²+4).
Herzliche Grüße,
Willy
Es muss vorne nur +1 heißen, nicht -1, denn holst Du das Minuszeichen in den Zähler, steht da -(a-2) und das ist -a+2...
Ansonsten passt's.
Rechnet man sowas, wie hier, mit Parameter, dann ist meist die Frage, für welche a gibt es eine, keine oder zwei Nullstellen; denn mehr als bis hierhin kannst Du da nicht auflösen.
da is ein kleiner Rechenfehler
=-(a-2)/2=-a/2+1 Minus mal Minus ergibt Plus
=-a/2+1+/-Wurzel(a²/4+1) mehr geht nich
oder =-a/2+1+/- Wurzel(a²/4)*Wurzel(1+4/a²) bringt nix
Sieht doch gut aus, bis auf einen Vorzeichenfehler im Ausdruck vor der Wurzel.
Was ist denn der Vorzeichenfehler? Update: Habs gefunden ! Danke
Wie soll ich die Wurzel ziehen bei a^2/4 ? Ist das einfach a/2 ?