Physik Freier Fall Diagramm?
Kann mir jemand erklären, warum bei einem freien Fall die Geschwindigkeit negativ ist und warum die Geschwindigkeit abnimmt? Und warum ist beim t-h-Diagramm die Parabel nach unten geöffnet?
3 Antworten
Hallo leikexxx,
die Geschwindigkeit (engl. velocity) ist eigentlich ein sogenannter Vektor
v› = (v.x; v.y; v.z) = (Δx/Δt; Δy/Δt; Δz/Δt);
was wir oft auch Geschwindigkeit nennen, ist eigentlich nur deren Betrag
|v›| = √{v.x² + v.y² + v.z²},
das Tempo (engl. speed); v.x, v.y und v.z werden als die Komponenten von v› bezeichnet. Üblich ist, v.x und v.y als horizontale und v.z als (lokal, da die Erde ja nicht flach ist) vertikale Komponenten zu interpretieren. Negative Werte stehen für Bewegungen gegen die Achsenrichtung.
Beim senkrechten freien Fall (anders als beim Wurf) ist nur v.z im Spiel. Die z-Achse wird üblicherweise als nach oben gerichtet definiert, was v.z automatisch negativ macht. Dabei nimmt v.z noch ab (bis zum Aufprall natürlich), nicht jedoch |v›|. Man kann auch allgemeiner sagen, v.z entfernt sich immer weiter von 0.
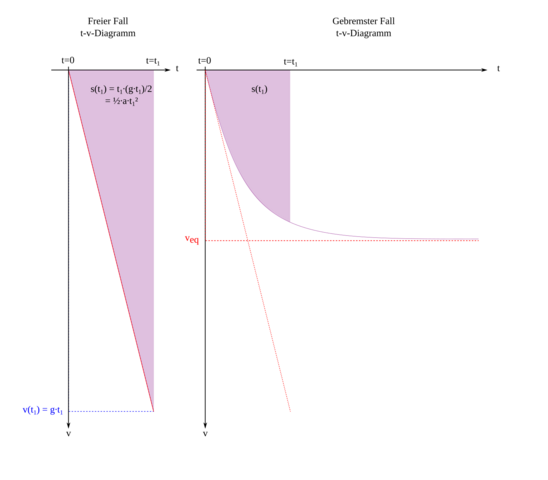
Frei ist der Fall übrigens streng genommen nicht (nur näherungsweise), wegen des Luftwiderstandes. Den Unterschied stelle ich in folgendem t - v.z - Diagramm dar:
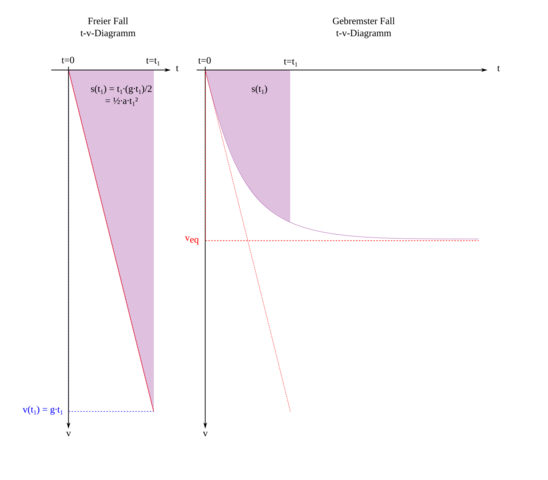
Und warum ist beim t-h-Diagramm…
Respektive t-z-Diagramm, dann kann man mit h die Höhe bezeichnen, aus der man einen Gegenstand fallen lässt.
…die Parabel nach unten geöffnet?
Siehe oben. Übrigens ist das streng genommen gar keine Parabel (und wäre es auch ohne Luftwiderstand nicht), eben weil die Erde nicht flach ist. Genau genommen ist es ein Bogen einer Ellipse, die sich komplettieren ließe, wenn man die Erde durch einen Massenpunkt gleicher Masse in ihrem Schwerpunkt ersetzte ¹), wobei unser Gegenstand im Perizentrum, am zum Massenpunkt nächsten Punkt der Bahn, natürlich durch immense Gezeitenkräfte zerrissen würde.
----------------
¹) Eigentlich stimmt selbst das wegen der starken Krümmung der Raumzeit in der Nähe des Massenpunktes nicht, aber man kann sich ja vorstellen, dass der Abstand im Perizentrum noch immer hinreichend weit entfernt sei, um diesen Effekt klein zu halten.
Das ist zunächst mal nur eine Frage der Festlegung und der Konventionen.
Wenn man den Nullpunkt beim freien Fall dorthin legt, wo man den Gegenstand loslässt, bewegt er sich im Koordinatensystem nach unten. Nach unten, also unterhalb der x-Linie, wird immer negativ angegeben. Dementsprechend muss auch die Geschwindigkeit negativ sein. Das Vorzeichen gibt einfach nur die Richtung an. Der Betrag der Geschwindigkeit nimmt allerdings im Quadrat zu.
Dementsprechend ist auch die Parabel nach unten geöffnet.
Theoretisch ja, das würde aber den üblichen Konventionen widersprechen.
Die Parabel ginge innerhalb der Konventionen auch dann nach oben, wenn man nur den Betrag der Geschwindigkeit auftragen würde.
Kleine Korrektur, da habe ich mich vertan...es ging ja um das t-h Diagramm. Also: streiche Geschwindigkeit und setze Fallhöhe h.
Die Geschwindigkeit in Abhängigkeit der Zeit wäre eine Gerade.
- weil das Koordinatensystem entgegen der Bewegung, nach oben, zeigt.
- weil das Objekt beschleunigt, die Geschwindigkeit vom Betrag her also größer wird.
- siehe 1. und 2.: es zeigt einfach die Flugbahn, wobei oben oben ist.
Ich verstehe 2. nicht so ganz, denn die Beschleunigung ist ja negativ, d.h die Geschwindigkeit nimmt ab oder?
Das heißt, die Parabel kann genauso gut nach oben geöffnet sein? Wenn sich die y-Achse nach unten orientiert, also nicht wie im Normalfall nach oben?