Parallelogramm Seitenlänge?
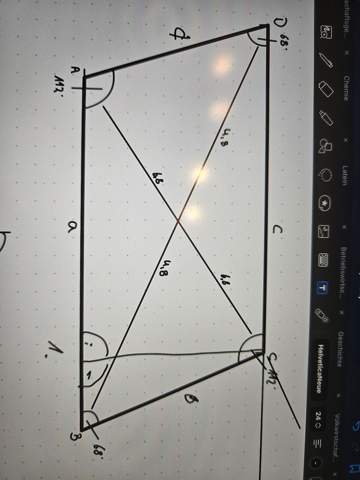
Hallo. Ich habe die Winkel und die Länge der Diagonalen. Also e = 13,6cm. F = 9,6
Winkel Alpha 112°
Beta 68°
Wie komme ich auf die Seitenlängen a und b?
3 Antworten
e² - f² = 4 * a * b * cos(β)
13,6^2 - 9,6^2 = 4 * a * b * cos(68)
13,6^2 - 9,6^2 = 4 * a * b * 0,374606593416
184,96 - 92,16 = 4 * a * b * 0,374606593416
92,8 = 4 * a * b * 0,374606593416
92,8 = 4ab * 0,374606593416
---
e² + f² = 2a²+2b²
e² + f² = (2 * a²)+ (2 * b²)
(13,6^2 + 9,6^2) = (2 * a²)+ (2 * b²)
(13,6^2 + 9,6^2) / 2 = a² +b²
(184,96 + 92,16) / 2 = a² + b²
277,12 / 2 = a² + b²
138,56 = a² + b²
------
Gleichung mit 2 Unbekannte
mit Gleichsetzungsverfahren
a = 6,183 cm ; b = 10,017 cm
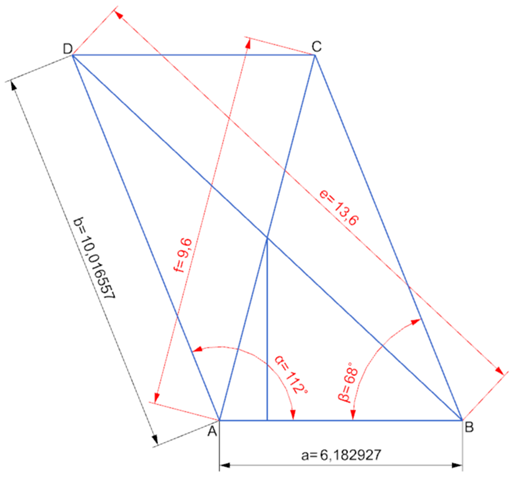
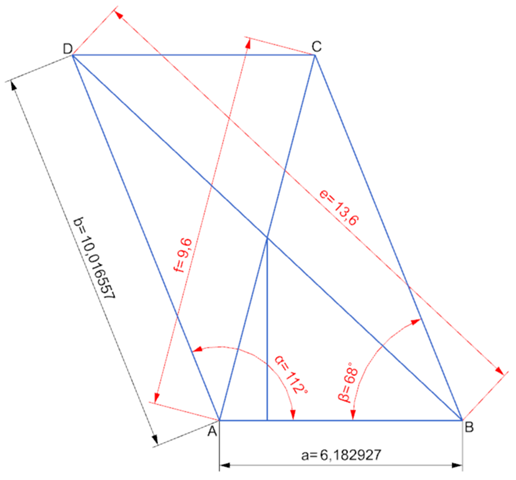
In einem Parallelogramm sind die Diagonalen gleichzeitig auch Symmetrieachsen und somit Winkelhalbierende von alpha bzw. beta. Damit kannst du nun die eingezeichnete Höhe berechnen: sin(alpha/2)=h/e.
Die Strecke a ist ja nun durch die eingezeichnete Höhe geteilt. Den linken Teil kannst du wie oben mit dem Kosinus berechnen. Den rechten Teil mit dem Tangens von beta und der berechneten Höhe.
Für die Seite b reicht der Satz des Pythagoras, aber wenn der nicht mehr so präsent ist, gehts wahlweise auch mit dem Sinus oder Kosinus von beta.
Falls die Winkel oder die Diagonalen vertauscht sind, komme ich an a = 10,02 und b = 6,18.