Mathe Aufgabe 2. Ableitung Wendepunkte?
Hallo ich brauche Hilfe bei der Nr. 2) b)
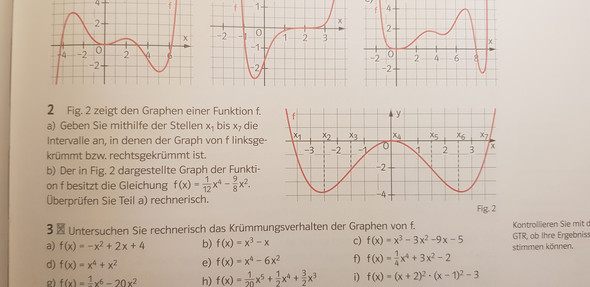
Ich habe W1=-2,29 also links-rechts gekruemmt ; W2=5 also rechts-links ; und bei W3 habe ich das selbe wie bei W2 raus aber ich kann mein Fehler nicht finden. Wahrscheinlich habe ich auch alles komplett falsch gerechnet 🤦♀️ (Btw das sind keine Hausaufgaben, ich wohne in NRW und habe Sommerferien)
5 Antworten
Nein, so rechnet man auch nicht. Wir machen die Aufgabe mal zusammen. Weißt du wie man Wendepunkte bestimmst, was das überhaupt ist? Wie bestimmt man das Krümmungsverhalten?
sorry hab da was verwechselt. Man muss auch die 3. Ableitung machen. Die 2. Ableitung setzt man =0 und die Werte die herauskommen setzt man dann in die 3. Ableitung
Sorry ist bisschen anstrengend mit mir hahah ich versuch mir das alles selbst beizubringen aber hab mich nur selbst verwirrt
Kein Wunder das du in der Klemme steckst, das stimmt ja auch nicht was du dachtest.
Die Ableitung gibt die Steigung an jedem Punkt des Graphen an. Dabei gibt f‘(x) oder f^1(x) die Steigung von f(x) oder f^0(x) an.
Suchst du Extremas also den höchsten oder niedrigsten Punkt in der unmittelbaren Umgebung so musst du f‘(x) = 0 setzen, denn die Ableitung einer Stelle x0 ist definiert durch den Grenzwert des Differenzenquotienten
lim ( f(x) - f(x0)/(x-x0) und das ist die Tangentensteigung.
x1-> x0
Die Tangente ist also die Ableitung an einem Punkt x0. Bei einem Extrema ist die Steigung 0 was man an einem Graphen sehr gut sehen kann. Steigung = Ableitung also gilt deswegen f‘(x) = 0. Da es aber auch nicht nur eine Art Extrema gibt, sondern Hoch,Tief und Sattelpunkte die auch eine horizontale Tangente aufweisen können, musst du die Steigung der Ableitung untersuchen die gibt ja auch die Krümmung an. Ist f‘‘(x) > 0 -> Tiefpunkt, denn hier wird die Steigung erstmal negativ und dann positiv also > 0. Ist f‘‘(x) < 0 ist die Steigung erstmal positiv, aber dann negativ. Deswegen setzt du deine gefundenen Werte in f‘‘(x) ein. Musst du aber nicht f‘(x) würde auch reichen, du müsstest halt eine Intervallpunktierung machen.
Für einen Wendepunkt gilt f‘‘(x) = 0 , da f‘‘(x) das Krümmungsverhalten angibt und bei einem Wendepunkt ist die Krümmung gleich 0. Um zu prüfen ob es sich um ein Wendepunkt handelt müsstest du noch f‘‘‘(x) bilden, aber manchmal versagt das auch...
Um das Krümmungsverhalten einer Funktion zu bestimmen gelten folgende Bedingungen:
f‘‘(x) > 0 —-> linksgekrümmt
f‘‘(x) < 0 —-> rechtsgekrümmt
Für einen Wendepunkt gilt :
f‘‘(x) = 0
f‘‘‘(x) > 0 —-> RL Wendepunkt
f‘‘‘(x) < 0 —-> LR Wendepunkt
Warum gilt das untere?
Wenn du dir eine Funktion f(x) = ax^3 + bx^2+cx+d mit a u 0 anschaust wirst du folgendes feststellen. Diese Funktion kann maximal nur einen Wendepunkt haben. Also perfekt um die Bedingungen herzuleiten.
Bei einem Wendepunkt ändert sich die Krümmung von konvex zu konkav oder zu konkav zu konvex.
Ist also der Graph zuerst linksgekrümmt dann ist der Graph nach dem Wendepunkt rechtsgekrümmt die Steigung der Steigung von f‘‘(x) also f‘‘‘(x) ist < 0 , also gilt f‘‘‘(x) < 0 für LR W.
Ist der Graph hingegen rechtsgekrümmt und nach dem Wendepunkt linksgekrümmt ist die Steigung von f‘‘‘(x) > 0 also gilt RL W.
Merke :
f(x) <- f‘(x) -> f‘‘(x) <- f‘‘‘(x)
Steigung von f(x) Steigung von f‘‘(x)
Also zusammengefasst folgende Bedingungen:
Notwendige Bedingung für ein Extrema :
f‘(x) = 0
Hinreichende Bedingung:
f‘‘(x) > 0 -> Tiefpunkt
f‘‘(x) < 0 -> Hochpunkt
Notwendige Bedingung für eine Wendestelle :
f‘‘(x) = 0
Hinreichende Bedingung:
f‘‘‘(x) u 0
f‘‘‘(x) > 0 -> RL W
f‘‘‘(x) < 0 -> LR W
Sieht doch schon ein bisschen geordneter aus.
Als Beispiel für Bedingung 1 könnte man f(x) = x^2+4x+3, x € IR nehmen.
f(x) = x^2+4x+3
f‘(x) = 2x + 4
f‘‘(x) = 2
2x + 4 = 0
2x = -4
x = -2
f‘‘(-2) = 2 > 0 -> Tiefpunkt
f(-2) = (-2)^2+4*(-2)+3 = -1
TP(-2/-1)
Und weil der Tiefpunkt auch nur ein Punkt auf dem Graphen ist :
-1 = (-2)^2 + 4*(-2)+3
-1 = 4 - 8 + 3
-1 = -1 Wunderbar
Beispiel für Bedingung 2 :
f(x) = -x^3+3x+2, x € IR
f(x) = -x^3 + 3x + 2
f‘(x) = -3x^2 + 6
f‘‘(x) = -6x
f‘‘‘(x) = -6
-6x = 0
x = 0
f‘‘‘(0) = -6 < 0 -> LR W
f(0) = -0^3 + 3*0 + 2 = 2
LR - W (0/2)
Und :
2 = -0^3 + 3*0 + 2
2 = 2
Wie gesagt wir können die Aufgabe noch gemeinsam angehen.
Danke für deine Mühe!! Mit Beispielen lerne ich viel schneller Hahah Hab jetzt alles verstanden und zurueck zu meiner Aufgabe: f"(x)= 12/144x^2-9/4 = 0 (man tut die 9/4 auf die andere seite und dann nimmt man die +-wurzel vom ergebnis also) x1=1,5 und x2=-1.5 danach habe ich die beiden x-Werte in f' ' '(x)= 2x eingesetzt da kam raus 3>0 also RL W und -3<0 LR W
Aber der @fjf100 hat bei den x-Werten irgendwas mit 2,1... raus
Überprüfe durch Punktprobe!
x1 = 1,5 x2 = -1,5 wegen f(x) = f(-x)
f‘‘‘(x) = 2x
f‘‘‘(1,5) = 3 > 0 —-> RL W
f‘‘‘(-1.5) = -3 < 0 —-> LR W
Also haben wir : f(1,5) = -135/64= -2,109 und das wegen oben auch für x2.
RL-W(3/2 | -135/64) und LR - W (-1,5|-135/64)
Und jetzt Probe :
-135/64 = 1/12*(3/2)^4 - 9/8*(3/2)^2
-135/64 = -135/64
-135 = 1/12 * (-3/2)^4 - 9/8*(-3/2)^2
-135/64 = -135/64
Stimmt alles! Herzlichen Glückwunsch du hast die Analysis verstanden, nur an deiner Formulierung müssen wir arbeiten ;).
Sei die Notation wie in der Angabe. P=(x,y) ist Wendepunkt von G_f genau dann wenn f^{(2)}(x)=0 und f^{(3)}\neq 0. Zu finden ist also zuerst die Nullstellenmenge durch Nullsetzen der zweiten Ableitung des Ausdrucks f(x). Anschließend verifiziere man, dass für jeden Wert von x in jener Menge die dritte Ableitung von f an dieser Stelle von 0 verschieden ist. Die Ableitungen sind schnell gefunden f(x)=x^4/12-9/8*x^2 => f'(x)=x^3/3-9/4*x=>f''(x)=x^2-9/4 => f'''(x)=2*x. Nullsetzen der zweiten Ableitung liefert x = 3/2 oder x= -3/2. Da der Absolubetrag in beiden Fällen von 0 verschieden ist, folgt aus f'''(x)=2*x linear sofort, dass die dritte Ableitung von f für jeden der beiden Werte von x von 0 verschieden ist. Damit liefert das obige notwendige und hinreichende Kriterium für Wendepunkte, dass die Menge W der Wendepunkte gegeben ist durch W={(-3/2,f(-3/2)),(3/2,f(3/2))}. Es ist leicht zu sehen, dass für beliebige x in R gilt f(x)=f(-x), so dass insbesondere f(3/2)=f(-3/2). Damit ergibt sich f(3/2)=3^4/(2^6*3)-3^4/2^5 = (-2*3^4+3^3)/2^6 =(-162+27)/(64)=-135/64. Per Augenmaß stimmt das gant gut mit dem Wert aus der Graphik überein, sollte aber nochmal in Ruhe nachgerechnet werden. Damit finden wir W = {(-3/2,-135/64),(3/2,-135/64)}.
VG
dongodongo
siehe Mathe-Formelbuch,was man privat in jeden Buchladen bekommt, "Kurvendiskussion"
Bedingung "Wendepunkt" f´´(x)=0 und f´´´(x) ungleich Null
f(x)=1/12*x^4-9/8*x^2 abgeleitet
f´(x)=4/12*x^3-18/8*x=1/3-9/4*x
f´´(x)=0=3/3*x^2-9/4=x^2-9/4 Nullstellen bei x1,2=+/- Wurzel(9/4)=+/- 2,1213..
also bei x1=2,1213 und x2=-2,1213 es gibt nur diese 2 Wendepunkte
f´´´(x)=2*x ungleich NULL
Der Wendepunkt trennt 2 Kurvenbögen (konkav/konvex)
Krümmung k=y´´/(1+(y´)^2)^(3/2)
von oben "konvex" (Rechtskrümmung) wenn k<0
"konkav" (Linkskrümmung) wenn k>0
y´´=f´´(x) ist die 2.te Ableitung von f(x)
k<0 wenn y´´=f´´(x)=negativ
k>0 wenn y´´=f´´(x)=positiv
Nimm es nicht persönlich, aber Bedingungen rein klatschen finde ich nicht gut. Der Schüler/in soll das Thema 100% verstehen und sich nicht an Bedingungen angeln, schlimmer auswendig lernen.
Aber sag mal was für eine Formelsammlung benutzt du denn?
Mein Mathe-Formelbuch hat 580 Seiten mit Formeln,Zeichnungen und kleinen Beispielaufgaben.
"Taschenbuch Mathematischer Formeln" Bartsch, Verlag Harri Deutsch Thun und FrankfurtMain
VEB 8Volkseigener Betrieb) Fachbuchverlag Leipzig 1985 ,gibt´s net mehr
Alleine Kapitel "trigonometrische Funktionen" sind 10 Seiten mit Formeln.
Kann man gar nicht alle auswendig lernen.
Hinweis: Bedingung Wendepunkt ist nun mal f´´(x)=0 und f´´´(x) ungleich Null.
Ohne dieses Wissen,kann man das nicht rechnen.
Ich habe 186 "hilfreichste Antworten" von den Schülern bekommen.
Meine Erklärungen waren besser,als die der Pauker in der Schule!!
Du bildest zuerst die Ableitung der Funktion. Diese stellt die Steigung der Funktion dar. Nur wenn die Steigung 0 wird kann es einen Wendepunkt geben. Also setzst du die Ableitung gleich 0 und bestimmst die Lösung (Nullstellen) der Gleichung. Falls die Ableitung vor dem Nullpunkt ein anderes Vorzeichen hat, als danach, so liegt ein Wendepunkt vor, ansonsten ein Sattelpunkt.
Durch Ausklammen von Binomen kannst du auch Nullstellen finden.
die Kurve hat doch nur 2 Wendepunkte
f ' ' = 0 dann bekommst du die 2 x-Werte der beiden Wendepunkte
dann
https://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/kruemmung-und-wendepunkt
Also ich habe es so verstanden dass man um ein Wendepunkt zu bestimmen erstmal die 1. und 2. Ableitung macht danach setzt man die erste Ableitung =0 und die Werte setzt man dann in die 2. Ableitung um zu gucken ob es rechtslinks oder linksrechts gekruemmt ist